UVa 11538 象棋中的皇后

https://vjudge.net/problem/UVA-11538

题意：

n×m的棋盘，有多少种方法放置两个相互攻击的皇后？

思路：

这两个皇后互相攻击的方式只有3种，在同一行，在同一列，或在同一对角线。因为每种情况没有交集，所以可以用加法原理。

先考虑同一行，每一行都有种放法，共有n行，所以就是n×m×(m-1)。

列与行的情况是相同的。

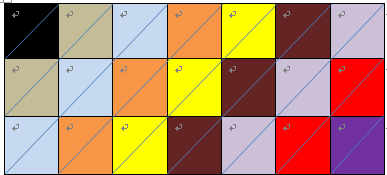
考虑对角线，如图，从左到右对角线的长度为1,2,3,...n-1,n,n...n(m-n+1个n),n-1,n-2,...2,1

因为还有另一个对角线的情况，所以结果要乘以2，最后等于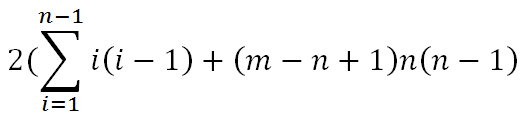

最后化简即可。

 #include<iostream>
 #include<cstdio>
 #include<cmath>
 #include<cstring>
 #include<queue>
 using namespace std;

 int main()
 {
    // freopen("D:\\input.txt", "r", stdin);
     long long n,m;
     while(cin>>n>>m && n && m)
     {
         if(n>m)  swap(n,m);
         cout<<n*m*(m+n-)+*n*(n-)*(*m-n-)/<<endl;
     }
     return ;
 }