估计人数【最小路径重复点覆盖】【直接在（i，j）建一个新点】

估计人数

题意

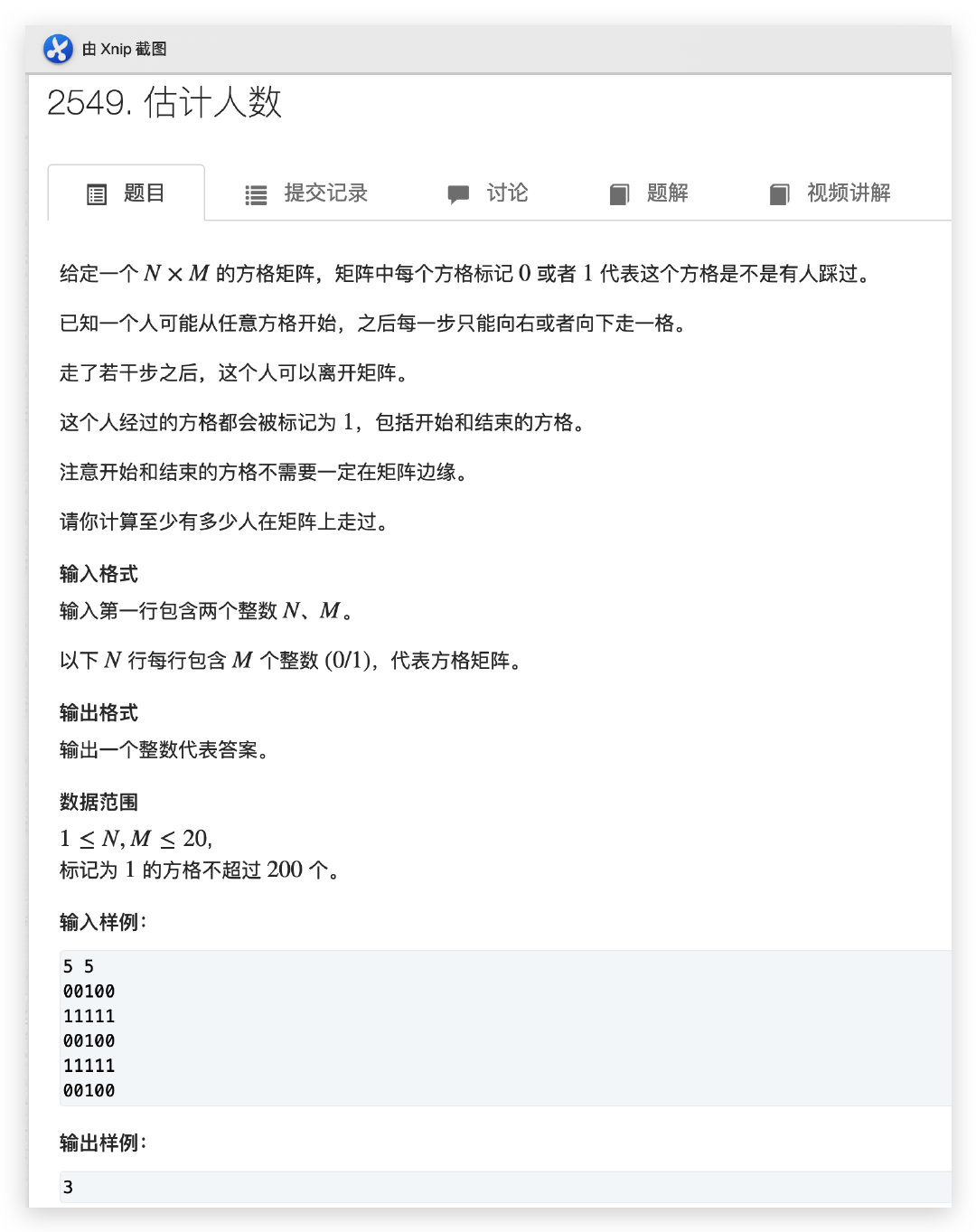
思路

用最少的人，走完这几条线。最小重复路径点覆盖问题

建图之后，跑一下二分图。

考虑建图：图中‘1’连着完下、或者右走。我们把图中所有的1编号，然后建图，然后floly，然后匈牙利。

代码

#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define mst(s,_s) memset(s, _s, sizeof(s))
const double PI = acos(-1.0);
const double eps = 1e-6;
const int INF = 0x3f3f3f3f;
const int N = 1e6+100;
int T,n,m;
char t[300][300];
int h[N],ne[N],e[N],idx;
void add(int a,int b)
{
    e[idx]=b;
    ne[idx]=h[a];
    h[a]=idx++;
}
int num[300][300],cnt;
int g[300][300];

int st[N],match[N];

int find(int x)
{
    for(int i=1;i<=n;i++)
    {
        if(!g[x][i]) continue;
        if(st[i]) continue;
        st[i]=1;
        if(!match[i] || (match[i] && find(match[i])))
        {
            match[i]=x;
            return true;
        }
    }
    return false;
}
int main() {
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>t[i]+1;
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
        {
            if(t[i][j]=='1')
            {
                num[i][j]=++cnt;
            }
        }

    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=m;j++)
        {
            if(num[i][j] && num[i][j+1])
                g[num[i][j]][num[i][j+1]]=1;
            if(num[i][j] && num[i+1][j])
                g[num[i][j]][num[i+1][j]]=1;
        }
    }

    n=cnt;
    for(int k=1;k<=n;k++)
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
                g[i][j]|=g[i][k]&g[k][j];

    int res=0;
    for(int i=1;i<=n;i++)
    {
        memset(st,0,sizeof st);
        if(find(i))
            res++;
    }
    cout<<n-res<<endl;

    return 0;
}