分布式机器学习：PageRank算法的并行化实现（PySpark）

1. PageRank的两种串行迭代求解算法

我们在博客《数值分析：幂迭代和PageRank算法(Numpy实现)》算法中提到过用幂法求解PageRank。

给定有向图

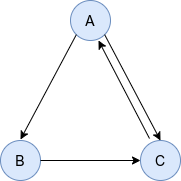
我们可以写出其马尔科夫概率转移矩阵\(M\)(第\(i\)列对应对\(i\)节点的邻居并沿列归一化)

\[\left(\begin{array}{lll}
0 & 0 & 1 \\
\frac{1}{2} & 0 & 0 \\
\frac{1}{2} & 1 & 0
\end{array}\right)
\]

然后我们定义Google矩阵为

\[G=\frac{q}{n} E+(1-q) M
\]

此处\(q\)为上网者从一个页面转移到另一个随机页面的概率（一般为0.15），\(1-q\) 为点击当前页面上链接的概率，\(E\)为元素全1的\(n\times n\) 矩阵( \(n\) 为节点个数)。

而PageRank算法可以视为求解Google矩阵占优特征值（对于随机矩阵而言，即1）对应的特征向量。设初始化Rank向量为 \(x\)（ \(x_i\) 为页面\(i\)的Rank值），则我们可以采用幂法来求解：

\[x_{t+1}=G x_{t}
\]

(每轮迭代后要归一化)

现实场景下的图大多是稀疏图，即\(M\)是稀疏矩阵。幂法中计算 \((1-q)Mx_t\) ，对于节点 \(i\) 需使用reduceByKey()（key为节点编号）操作。计算 \(\frac{q}{n}{E}x_t\) 则需要对所有节点的Rank进行reduce()操作，操作颇为繁复。

PageRank还有一种求解算法（名字就叫“迭代算法”），它的迭代形式如下：

\[x_{t+1} = \frac{q}{n}\bm{1} + (1-q)Mx_t
\]

可以看到，这种迭代方法就规避了计算 \(\frac{q}{n}Ex_t\)，通信开销更小。我们接下来就采用这种迭代形式。

2. 图划分的两种方法

目前对图算法进行并行化的主要思想是将大图切分为多个子图，然后将这些子图分布到不同的机器上进行并行计算，在必要时进行跨机器通信同步计算得出结果。学术界和工业界提出了多种将大图切分为子图的划分方法，主要包括两种，边划分(Edge Cut)和点划分(Vertex Cut)。

2.1 边划分

如下图所示，边划分是对图中某些边进行切分。具体在Pregel^[1]图计算框架中，每个分区包含一些节点和节点的出边；在GraphLab^[2]图计算框架中，每个分区包含一些节点、节点的出边和入边，以及这些节点的邻居节点。边划分的优点是可以保留节点的邻居信息，缺点是容易出现划分不平衡，如对于度很高的节点，其关联的边都被划分到一个分区中，造成其他分区中的边可能很少。另外，如下图最右边的图所示，边划分可能存在边冗余。

2.2 点划分

如下图所示，点划分是对图中某些点进行切分，得到多个图分区，每个分区包含一部分边，以及与边相关联的节点。具体地，PowerGraph^[3]，GraphX^[4]等框架采用点划分，被划分的节点存在多个分区中。点划分的优缺点与边划分的优缺点正好相反，可以将边较为平均地分配到不同机器中，但没有保留节点的邻居关系。

总而言之，边划分将节点分布到不同机器中(可能划分不平衡)，而点划分将边分布到不同机器中(划分较为平衡)。接下来我们使用的算法为类似Pregel的划分方式，使用边划分。我们下面的算法是简化版，没有处理悬挂节点的问题。

3. 对迭代算法的并行化

我们将Rank向量用均匀分布初始化（也可以用全1初始化，不过就不再以概率分布的形式呈现），设分区数为3，算法总体迭代流程可以表示如下：

注意，图中flatMap()步骤中，节点\(i\)计算其contribution（贡献度）：\((x_t)_i/|\mathcal{N}_i|\)，并将贡献度发送到邻居集合\(\mathcal{N}_i\)中的每一个节点。之后，将所有节点收到的贡献度使用reduceByKey()（节点编号为key）规约后得到向量\(\hat{x}\)，和串行算法中\(Mx_t\)的对应关系如下图所示：

并按照公式\(x_{t+1} = \frac{q}{n} + (1-q)\hat{x}\)来计算节点的Rank向量。然后继续下一轮的迭代过程。

4. 编程实现

用PySpark对PageRank进行并行化编程实现，代码如下：

import re
import sys
from operator import add
from typing import Iterable, Tuple

from pyspark.resultiterable import ResultIterable
from pyspark.sql import SparkSession

n_slices = 3  # Number of Slices
n_iterations = 10  # Number of iterations
q = 0.15 #the default value of q is 0.15

def computeContribs(neighbors: ResultIterable[int], rank: float) -> Iterable[Tuple[int, float]]:
    # Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
    num_neighbors = len(neighbors)
    for vertex in neighbors:
        yield (vertex, rank / num_neighbors)

if __name__ == "__main__":
    # Initialize the spark context.
    spark = SparkSession\
        .builder\
        .appName("PythonPageRank")\
        .getOrCreate()

    # link: (source_id, dest_id)
    links = spark.sparkContext.parallelize(
        [(1, 2), (1, 3), (2, 3), (3, 1)],
        n_slices
    )                       

    # drop duplicate links and convert links to an adjacency list.
    adj_list = links.distinct().groupByKey().cache()

    # count the number of vertexes
    n_vertexes = adj_list.count()

    # init the rank of each vertex, the default is 1.0/n_vertexes
    ranks = adj_list.map(lambda vertex_neighbors: (vertex_neighbors[0], 1.0/n_vertexes))

    # Calculates and updates vertex ranks continuously using PageRank algorithm.
    for t in range(n_iterations):
        # Calculates the contribution(rank/num_neighbors) of each vertex, and send it to its neighbours.
        contribs = adj_list.join(ranks).flatMap(lambda vertex_neighbors_rank: computeContribs(
            vertex_neighbors_rank[1][0], vertex_neighbors_rank[1][1]  # type: ignore[arg-type]
        ))

        # Re-calculates rank of each vertex based on the contributions it received
        ranks = contribs.reduceByKey(add).mapValues(lambda rank: q/n_vertexes + (1 - q)*rank)

    # Collects all ranks of vertexs and dump them to console.
    for (vertex, rank) in ranks.collect():
        print("%s has rank: %s." % (vertex, rank))

    spark.stop()

运行结果如下：

1 has rank: 0.38891305880091237.
2 has rank: 0.214416470596171.
3 has rank: 0.3966704706029163.

该Rank向量与我们采用串行幂法得到的Rank向量 \(R=(0.38779177,0.21480614,0.39740209)^{T}\) 近似相等，说明我们的并行化算法运行正确。

参考

• [1] Malewicz G, Austern M H, Bik A J C, et al. Pregel: a system for large-scale graph processing[C]//Proceedings of the 2010 ACM SIGMOD International Conference on Management of data. 2010: 135-146.

• [2] Low Y, Gonzalez J, Kyrola A, et al. Distributed graphlab: A framework for machine learning in the cloud[J]. arXiv preprint arXiv:1204.6078, 2012.

• [3] Gonzalez J E, Low Y, Gu H, et al. {PowerGraph}: Distributed {Graph-Parallel} Computation on Natural Graphs[C]//10th USENIX symposium on operating systems design and implementation (OSDI 12). 2012: 17-30.

• [4] Spark: GraphX Programming Guide

• [5] GiHub: Spark官方Python样例

• [6] 许利杰，方亚芬. 大数据处理框架Apache Spark设计与实现[M]. 电子工业出版社, 2021.

• [7] Stanford CME 323: Distributed Algorithms and Optimization (Lecture 15)

• [8] wikipedia: PageRank