数字图像处理-基于matlab-直方图均匀化,傅立叶变换,图像平滑,图像锐化

直方图均匀化

任务：用MATLAB或VC或Delphi等实现图像直方图均匀化的算法。

clc;clear;close all;  % 清除工作台 %
path(path,'..\pics');  % 设置路径 %
im=imread('AT3_1m4_01.tif'); % 读取图像 %
figure(1);imshow(im);  % 显示图像 原始图像 %

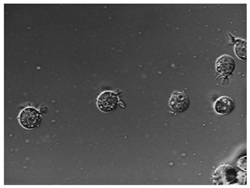
imD=double(im);  % 转为double类型 %
figure(3);  % 准备画板 %
[M,N]=size(im); % 得到图像长宽信息 %
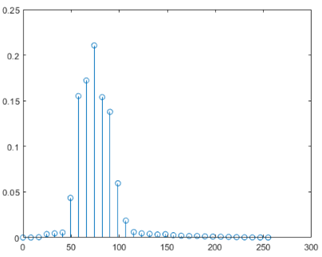
[counts,center]=imhist(im,32); % 将直方图均分为32个等级，默认为256个等级 %
counts=counts/(M*N);  % 归一化 %
stem(center,counts);  % 画图 图像像素分析 %

figure(4); % 准备画板 %
x=0:255;  % 生成0~255的向量 %
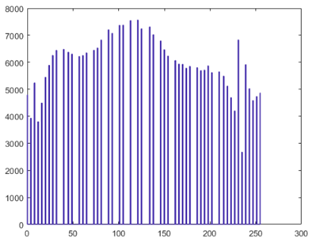
hist(im(:),x);  % 画直方图 像素分布 %

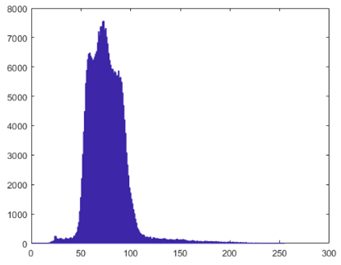
I=histeq(im);  % 直方图均衡化 %
figure(5);imshow(I);  % 显示图像 图像均衡化效果 %

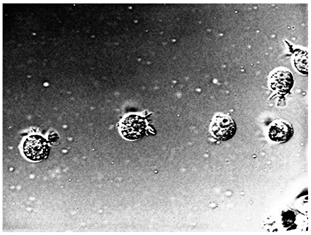
figure(6);  % 准备画板 %
hist(I(:),x); % 画直方图 均衡化的像素分布 %

傅立叶变换

任务：掌握傅立叶变换的基本原理和实现算法。

clc;clear;close all;  % 清除工作台 %
path(path,'..\pics');  % 设置路径 %
I=imread('greens.jpg');  % 读取图像 %
figure(1);imshow(I); % 显示图像 原始图像 %

sI=rgb2gray(I);  % 转换为灰度图 %
I=im2double(I);  % 转为double类型 %
figure(2);imshow(I,[0,1]);  % 显示图像 灰度化的图像 %

F=fft2(I);  % 傅里叶变换 %
Fm=abs(F); % 取绝对值 %
T=log(Fm+1); % 取log %
figure(3);imshow(T,[]); % 显示图像 快速傅里叶变化后的图像 %

Ff=fftshift(F); %对傅里叶变换后的图像进行象限转换
Fm=abs(Ff); % 取绝对值 %
T=log(Fm+1); % 取log %
figure(4);imshow(T,[]); % 显示图像 象限转换 %

J=ifft2(F);  % 快速傅里叶逆变换 %
figure(5);imshow(J,[0,1]); % 显示图像 快速傅里叶逆变化的图像 %

讨论不同的图像内容与频谱之间的对应关系.

​因为频谱图表示图像梯度的分布图，所以原图和频率图上的点不是一一对应的,频谱图上的点表示空域图某点的灰度梯度大小，梯度大其频率高,暗的点数多，就是说其原图像素梯度较小，频率低，图像就较柔和。

图像平滑

任务：掌握图像平滑算法的基本原理。

clc;clear;close all;  % 清除工作台 %
path(path,'..\pics'); % 设置路径 %
im=imread('pout.tif'); % 读取图像 %
im=double(im);  %  转换为double类型 %
im=im/max(im(:)); % 归一化 %
figure(1);imshow(im,[0,1]);title('ground truth'); % 显示图像 原始图像 %

P1 = imnoise(im,'gaussian',0,0.005); % 添加高斯噪声
figure(2);imshow(P1,[0,1]); title('gaussian noise'); % 显示噪声图像 添加高斯噪声 %

P2 = imnoise(im,'salt & pepper',0.02); % 添加椒盐噪声
figure(3);imshow(P2,[0,1]); title('salt& pepper noise');  % 显示噪声图像 添加椒盐噪声 %

a=[1 1 1;1 1 1;1 1 1];  % 建立3x3的全1的矩阵 %
template1=(1/9)*a;  % 模板 %
imAve=conv2(double(P1),double(template1));  % 卷积 %
figure(4);imshow(imAve,[0,1]); title('average filter'); % 显示图像 均值滤波 %

imMed=medfilt2(P1,[3,3],'symmetric');  % 中值滤波 %
figure(5);imshow(imMed,[0,1]);title('median filter'); % 显示图像 中值滤波 %

psf=fspecial('gaussian',3,1); % 生成高斯滤波器（也叫算子） %
imGau=imfilter(P1,psf,'conv','symmetric'); % 应用滤波 %
figure(6);imshow(imGau,[0,1]); title('gaussian filter'); % 显示图像 高斯滤波 %

图像锐化

任务: 掌握图像锐化算法的基本原理。

罗伯特算子(Roberts)实现

function [edge]= RobertsOperator(pic)
    edge = zeros(size(pic));

    h = size(pic, 1);
    w = size(pic, 2);

    for i = 1 : h - 1
        for j = 1 : w - 1
            edge(i, j) =abs(pic(i, j) - pic(i + 1, j + 1)) + abs(pic(i, j + 1) - pic(i + 1, j));
        end
    end
end

索贝尔算子(Sobel)实现

function [edge] = SobelOperator(pic)
    edge = zeros(size(pic));

    h = size(pic, 1);
    w = size(pic, 2);

    gx = [-1, -2, -1; 0, 0, 0; 1, 2, 1];
    gy = gx';

    for i = 2 : h - 1
        for j = 2 : w - 1
            sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
            g1 = abs(sum(sum(sub .* gx)));
            g2 = abs(sum(sum(sub .* gy)));
            if g1 > g2
                edge(i, j) = g1;
            else
                edge(i, j) = g2;
            end
        end
    end
end

普瑞维特算子(Prewitt)实现

function [edge] = PrewittOperator(pic)
    edge = zeros(size(pic));

    h = size(pic, 1);
    w = size(pic, 2);

    gx = [-1, -1, -1; 0, 0, 0; 1, 1, 1];
    gy = gx';

    for i = 2 : h - 1
        for j = 2 : w - 1
            sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
            g1 = abs(sum(sum(sub .* gx)));
            g2 = abs(sum(sum(sub .* gy)));
            if g1 > g2
                edge(i, j) = g1;
            else
                edge(i, j) = g2;
            end
        end
    end
end

二阶梯度算子(拉普拉斯算子-Laplace)实现

function [edge] = LaplaceOperator(pic)
    edge =zeros(size(pic));

    h = size(pic, 1);
    w = size(pic, 2);

    l = [0, 1, 0; 1, -4, 1; 0, 1, 0];

    for i = 2 : h - 1
        for j = 2 : w - 1
            sub = double(pic(i - 1 : i + 1, j - 1 : j + 1));
            d = sum(sum(sub .*l));
            edge(i, j) =d;
        end
    end
end

实验

clc;clear;close all;  % 清除工作台 %
path(path,'..\pics');  % 设置路径 %
im=imread('pout.tif'); % 读取图像 %
im=double(im);  % 转换为double类型 %
im=im/max(im(:));  % 归一化 %
figure(1);imshow(im,[0,1]);title('ground truth');  % 显示图像 原始图像 %

result=RobertsOperator(im); % Roberts边缘检测 %
result=result/max(result(:));  % 归一化 %
figure(2);imshow(result,[0,1]);title('Roberts'); % 显示检测图像 Roberts算子 %

result=SobelOperator(im);  % Sobel边缘检测 %
result=result/max(result(:)); % 归一化 %
figure(3);imshow(result,[0,1]);title('Sobel'); % 显示检测图像 Sobel边缘检测 %

result=PrewittOperator(im);  % Prewitt边缘检测 %
result=result/max(result(:));  % 归一化 %
figure(4);imshow(result,[0,1]);title('Prewitt');  % 显示边缘检测结果 Prewitt边缘检测 %

result=LaplaceOperator(im);  % Laplace边缘检测 %
result=result/max(result(:));  % 归一化 %
figure(5);imshow(result,[0,1]);title('Laplace'); % 显示边缘检测结果 Laplace边缘检测结果 %

简单实现梯度计算

function [Px,Py] = my_gradient(im)
[h, w] = size(im);
Px = zeros(h, w);
Py = zeros(h, w);
for i=2:h-1
   for j=2:w-1
       Px(i, j) = abs(im(i + 1, j)-im(i - 1, j));
       Py(i, j) = abs(im(i, j + 1)-im(i, j - 1));
   end
end