Docker--数据管理之Volumes

前言：我们知道docker容器内产生或修改的数据仅在该容器内有效，即容器关闭，其之前产生或修改的数据也就删除了，这明显不能满足我们大多数场景的需求。当然这只是默认，docker为我们提供了多种保存数据的方式。如下

方式一：Volumes--它是由docker管理和创建的(也是和Bind mounts主要区别bie),你可以在使用它之前创建也可以在启动容器的时候一起创建。在启动的时候不指定名称就是匿名volumes。更重要的是它支持volume drivers(驱动),这样就可以支持远程共享数据(这也是docker官方推荐使用的原因和Bing mounts的重要区别)

方式二：Bind mounts--和Volumes很相似，除上面提到的区别

方式三：tmpfs mounts--它并没有提供持久化的支持，只是提供的多个容器在主机内存共享数据的支持。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图解: Host-主机，Filesystem-主机的文件系统，Docker area - “/var/lib/docker/volumes/”目录 ，箭头->绑定方式

本次仅学习Volumes:方式，也是docker推荐的方式

一：简介Volumes的增删查方式

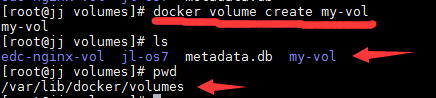
1.1 创建一个Volumes命名为my-vol 

　　docker volume create [my-vol]

1.2 查询列表(已创建的Volumes)

　　docker volume ls

1.3 查看

　　docker volume inspect [my-vol]

1.4 删除

　　docker volume rm [my-vol]

二：使用场景

　　场景假设：假设我的centos镜像，其根目录下有一个app目录，我在该目录下创建的任何数据我想让它持久保留(即:容器关闭或者死掉下次启动我仍能看到之前穿件的数据)，或者在多个容器之前共享该app目录下的内容。

步骤一： 创建Volumes并命名为my-vol

　　

步骤二：启动centos镜像，并绑定Volumes

　　docker run -d -it --name=1-OS --mount source=my-vol,target=/app2 centos

　　

note1:进入容器 ，查看根目录(),进入app2目录(即target目录)

　　docker exec -it 1-OS /bin/bash

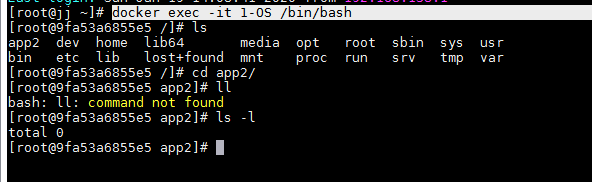
步骤三：校验Volumes是否绑定成功

　　docker inspect [容器ID或名字]

　　docker inspect 1-OS

　　

备注1：选择  --mount 

　　它是有多个键-值(key-value)对，并通过","分割组成的可用参数。

　　type - ： 指定绑定的类型，可选值有bind, volume, or tmpfs，默认是volume。

　　source - ：指定一个已创建的Volumes名字。因为Volumes指定了对应主机的那个目录去和容器

　　destination：指定容器的目录，用于与source目录对用

　　readonly：再议

　　volume-opt：再议

备注2：

检验1：在当前容器目录下创建一个文件(hello-volume.txt),并在主机目录下查看该文件

【1】在容器内创建

·

【2】在主机查看

校验2：另起一个容器，并绑定同一个数据卷(my-vol)，查看数据是否共用

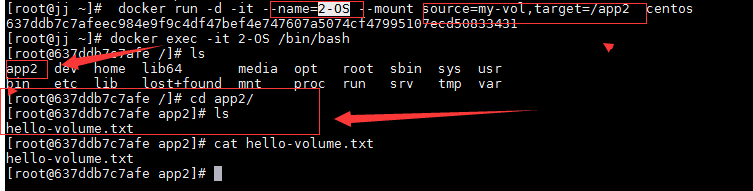
结论，另起的容器已共享Valumes数据

参考文档：https://docs.docker.com/storage/