sequence——强行推式子+组合意义

sequence

考虑长度<=x的方案数F(x)，然后(F(x)-F(x-1))*x贡献到答案里

n平方的做法可以直接DP，

感觉有式子可言，

就推出式子：类似coat，每个长度为i的计算i次。

再容斥下：

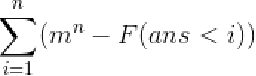
F是方案数，还是求：

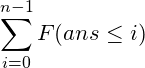
枚举分成的段数，枚举多少个超过i进行容斥：

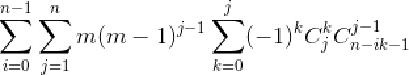
突破口：有个n-i*k-1，意味着i*k<=n，这样的i和k暴力枚举一共nlogn复杂度！

提出来，考虑干掉j

强行推式子：

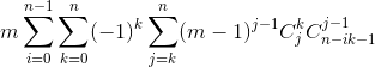
处理：

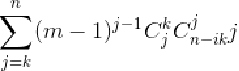
（怎么看怎么也看不出什么道理的样子）

来找组合意义吧：

有n-ik个球，我们先从中选出j个，再从选出的j个中选出k个。在j个球中我们选出一个特殊的球，对于剩下的球用m-1种颜色染色。

考虑讨论这个特殊的球是不是这k个球中的

即可得到;

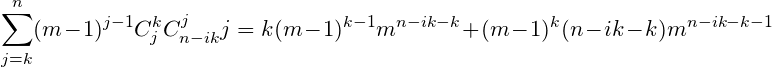（这里少写了C(n-i*k-k,k)）

预处理m-1的次幂和m的次幂和阶乘阶乘逆元

O(nlogn)

别忘了最后用n*m^n-

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define fi first
#define se second
#define mk(a,b) make_pair(a,b)
#define numb (ch^'0')
#define pb push_back
#define solid const auto &
#define enter cout<<endl
#define pii pair<int,int>
using namespace std;
typedef long long ll;
template<class T>il void rd(T &x){
    char ch;x=;bool fl=false;while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);(fl==true)&&(x=-x);}
template<class T>il void output(T x){if(x/)output(x/);putchar(x%+'');}
template<class T>il void ot(T x){if(x<) putchar('-'),x=-x;output(x);putchar(' ');}
template<class T>il void prt(T a[],int st,int nd){for(reg i=st;i<=nd;++i) ot(a[i]);putchar('\n');}

int mod;
namespace Modulo{
int ad(int x,int y){return (x+y)>=mod?x+y-mod:x+y;}
void inc(int &x,int y){x=ad(x,y);}
int mul(int x,int y){return (ll)x*y%mod;}
void inc2(int &x,int y){x=mul(x,y);}
int qm(int x,int y=mod-){int ret=;while(y){if(y&) ret=mul(x,ret);x=mul(x,x);y>>=;}return ret;}
}
using namespace Modulo;
namespace Miracle{
const int N=+;
int n,m;
int jie[N],inv[N];
int iv[N];
int m0[N],m1[N];
int C(int n,int m){
    if(n<||m<||n<m) return ;
    return mul(jie[n],mul(inv[m],inv[n-m]));
}
int main(){
    rd(n);rd(m);rd(mod);
    jie[]=;
    for(reg i=;i<=n;++i) jie[i]=mul(jie[i-],i);
    inv[n]=qm(jie[n],mod-);
    for(reg i=n-;i>=;--i) inv[i]=mul(inv[i+],i+);
    iv[]=;
    for(reg i=;i<=n;++i){
        iv[i]=mul(mod-mod/i,iv[mod%i]);
    }
    m0[]=m1[]=;
    for(reg i=;i<=n;++i){
        m0[i]=mul(m0[i-],m);
        m1[i]=mul(m1[i-],m-);
    }
    int ans=;
    for(reg i=;i<n;++i){
        for(reg k=;k<=n;++k){
            if(i*k+k>n) break;
            int tmp=;//
            if(k!=) tmp=ad(tmp,mul(C(n-i*k,k),mul(k,mul(m1[k-],m0[n-i*k-k]))));
            if(n-i*k-k->=) tmp=ad(tmp,mul(C(n-i*k,k),mul(m1[k],mul(m0[n-i*k-k-],n-i*k-k))));
            tmp=mul(tmp,(k&)?mod-:);
            tmp=mul(tmp,iv[n-i*k]);
            ans=ad(ans,tmp);
        }
    }
    ans=mul(ans,m);
    ans=ad(mul(n,qm(m,n)),mod-ans);
    ot(ans);
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
*/

突破口是i，k总共对数nlogn级别，干掉j用组合意义大力推导