[集训]Trominoes，钩子公式运用

题意

用这四种骨牌密铺n*m的正方形矩阵，可以不选，求方案数。n*m<=1E8。多组询问。

---

思考

用如上的表达难以进行计算，尝试转化为一种新的组合解释。

若从右上角开始填起，我们强制要求里面的轮廓线是单调增的。例如：

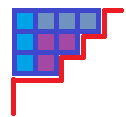这种方法既不影响合法性，又不会重复计数。

可以看见，我们只关心轮廓线的形状，不关心其他部分的细节，因此我们可以用长度为n+m的01串来表示其反向。在此处，默认01串从左下角向右上角写起，0代表上，1代表右。

每填充一个骨牌，可以发现这样的转移：

0001->1000

0011->1010

0101->1100

0111->1110

除了第四位上的数字，其余的三位在二进制表示下是完备的，也就是说，可以看做是单一的1先前移动了3位。

至此，原问题表述为：给定一个开头有n个1，末尾有m个0的字符串，每次可将1向前移动三位到一个字符为0的位置上，问构成开头有m个0，末尾有n个1的字符串的方案数有多少个。

该问题又可以划分为三个子问题，因为位置模3的余数不同的互不影响。也就是考虑若每次向右移动一个，有多少方案。

这个问题可以看做是经典的买票问题，使用钩子公式解决。复杂度O(n*m/3+T*n)

---

代码

 #include<bits/stdc++.h>
 #define mod 1000000007
 using namespace std;
 typedef long long int ll;
 ll fac[],n,m,T;
 void init()
 {
     fac[]=;
     for(int i=;i<=;++i)
         fac[i]=fac[i-]*i%mod;
 }
 ll qpow(ll x,ll y)
 {
     ll ans=,base=x;
     while(y)
     {
         if(y&)
             ans=ans*base%mod;
         base=base*base%mod;
         y>>=;
     }
     return ans;
 }
 inline ll C(int x,int y)
 {
     return fac[x]*qpow(fac[y],mod-)%mod*qpow(fac[x-y],mod-)%mod;
 }
 inline ll get(ll n,ll m)
 {
     ll ans=,sum=;
     for(int i=;i<=n;++i)
     {
         ans=ans*fac[i+m-]%mod;
         sum=sum*fac[i-]%mod;
 //        for(int j=1;j<=m;++j)
 //            ans=ans*(i+j-1)%mod;
     }
     return fac[n*m]*qpow(ans,mod-)%mod*sum%mod;
 }
 int main()
 {
     ios::sync_with_stdio(false);
     init();
     cin>>T;
     while(T--)
     {
         cin>>n>>m;
         if(n*m%!=)
         {
             cout<<<<endl;
             continue;
         }
         if(n%!=)
             swap(n,m);
         int base0=m/;
         int left0=base0,left1=base0+(m%>),left2=base0+(m%>);
         ll ans=get(n/,left0)*get(n/,left1)%mod*get(n/,left2)%mod;
         ans=ans*C((left0+left1+left2)*n/,left0*n/)%mod;
         ans=ans*C((left1+left2)*n/,left1*n/)%mod;
         cout<<ans<<endl;
     }
     return ;
 }