css3 matrix 矩阵

2D矩阵变换

matrix(1,0,0,1,0,0) 对应 matrix (a,b,c,d,e,f)

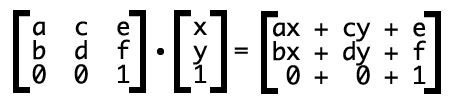
其中，x, y表示转换元素的所有坐标（变量）了,

3*3矩阵每一行的第1个值与后面1*3的第1个值相乘，第2个值与第2个相乘，第3个与第3个，然后相加

ax+cy+e为变换后的水平坐标，bx+dy+f表示变换后的垂直位置

偏移：e---水平偏移距离    f-----垂直偏移距离  css3单位px

现在，我们根据这个矩阵偏移元素的中心点，假设是(0, 0)，即x=0, y=0。

假设 x y 偏移30px

x坐标就是 ax+cy+e = *+*+ =
y坐标就是 bx+dy+f = *+*+ =

缩放：a---缩放X 水平     d----缩放Y垂直   css3单位 num

假设 s 代表 缩放

x' = ax+cy+e = s*x+0*y+0 = s*x;
y' = bx+dy+f = 0*x+s*y+0 = s*y;

也就是matrix(sx, 0, 0, sy, 0, 0);，等同于scale(sx, sy);

拉伸：b---拉伸Y垂直   c-----拉伸X 水平   css3单位弧度angle

matrix(,tan(θy),tan(θx),,,);

tanValY = Math.tan(deg * Math.PI / 180);
tanValX = Math.tan(deg * Math.PI / 180);

x' = x+y*tan(θx)+0 = x+y*tan(θx)  
y' = x*tan(θy)+y+0 = x*tan(θy)+y

对应于skew(θx + "deg"，θy+ "deg")这种写法

旋转：a   b  c d  4个值  css3单位弧度angle

matrix(cosθ,sinθ,-sinθ,cosθ,,)

cosVal = Math.cos(deg * Math.PI / 180);
sinVal = Math.sin(deg * Math.PI / 180);

x' = x*cosθ-y*sinθ+0 = x*cosθ-y*sinθ 
y' = x*sinθ+y*cosθ+0 = x*sinθ+y*cosθ

deg=30; //角度
cos=Math.cos(30 * Math.PI / 180); 
deg2=Math.acos(cos) * 180 / Math.PI; // 反三角函数

rotate(θdeg)这种书写形式要比matrix简单多了，首先记忆简单，其次，无需计算。例如，旋转30°

matrix表示则还要计算cos, sin值：transform: matrix(0.866025,0.500000,-0.500000,0.866025,0,0);

css3 直接： transform:rotate(30deg);

镜像对称效果：

轴围绕的那个点就是CSS3中transform变换的中心点，自然，镜像对称也不例外。因为该轴永远经过原点，因此，任意对称轴都可以用y = k * x表示

则matrix表示就是：

matrix((-k*k) / (+k*k), 2k / ( + k*k), 2k / ( + k*k), (k*k - ) / (+k*k), , )

如下图，已经y=kx，并且知道点(x, y)坐标，求其对称点(x’, y’)的坐标？

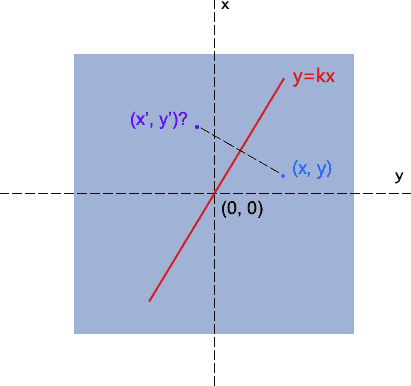
很简单，一是垂直，二是中心点在轴线上，因此有：

(y-y') / (x - x') = -/ k → ky-ky' = -x+x' //两条直线垂直,它们的斜率互为负倒数
(x + x') / 2 * k = (y + y')/ → kx+kx' = y+y'

很简单的，把x'和y'提出来，就有：

x' = (1-k*k)/(k*k+1) *x + 2k/(k*k+1) *y;
y' = 2k/(k*k+1) *x + (k*k-1)/(k*k+1) *y;

再结合矩阵公式：

x' = ax+cy+e;
y' = bx+dy+f;

我们就可以得到：

a = (-k*k)/(k*k+);
b = 2k/(k*k+);
c = 2k/(k*k+);
d = (k*k-)/(k*k+);

也就是上面matrix方法中的参数值啦！

3D变换中的矩阵

矩阵里头是从3*3变成4*4, 9到16,  2D 变换 加一个 Z轴

matrix3d(sx, 0, 0, 0, 0, sy, 0, 0, 0, 0, sz, 0, 0, 0, 0, 1)

perspective ：透视 --- 距离多远看图像

如果父元素 perspective ：200px ;（因为元素远去，我们眼睛看到的就会变小）；translateZ值越大，该元素也会越来越大，当translateZ值非常接近200像素，但是不超过200像素的时候 (如199像素)，该元素的大小就会撑满整个屏幕（如果父辈元素没有类似overflow:hidden的限制的话）。

perspective-origin眼睛看的位置,默认就是所看舞台或元素的中心 ,值为： left  center right length  % ; perspective-origin: x-axis y-axis;

transform-style: preserve-3d  表示3D透视

backface-visibility: hidden;   后面元素不可见