[开发技巧]·Python极简实现滑动平均滤波（基于Numpy.convolve）

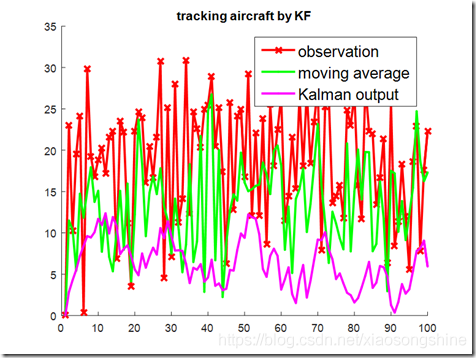
1.滑动平均概念

滑动平均滤波法（又称递推平均滤波法），时把连续取N个采样值看成一个队列，队列的长度固定为N ，每次采样到一个新数据放入队尾,并扔掉原来队首的一次数据.(先进先出原则) 把队列中的N个数据进行算术平均运算,就可获得新的滤波结果。N值的选取：流量，N=12；压力：N=4；液面，N=4~12；温度，N=1~4

优点：对周期性干扰有良好的抑制作用，平滑度高适用于高频振荡的系统

缺点：灵敏度低对偶然出现的脉冲性干扰的抑制作用较差不易消除由于脉冲干扰所引起的采样值偏差不适用于脉冲干扰比较严重的场合比较浪费RAM

2.解决思路

可以发现滑动平均滤波法计算很类似与一维卷积的工作原理，滑动平均的N就对应一维卷积核大小（长度）。

步长会有些区别，滑动平均滤波法滑动步长为1，而一维卷积步长可以自定义。还有区别就是一维卷积的核参数是需要更新迭代的，而滑动平均滤波法核参数都是一。

我们应该怎么利用这个相似性呢？其实也很简单，只需要把一维卷积核大小（长度）和N相等，步长设置为1，核参数都初始为1就可以了。由于一维卷积具备速度快，然后我们就可以使用一维卷积来实现这个功能了，快速高效。

使用深度学习框架实现这个功能是否有些大材小用了？是有些大材小用了，因为这里使用卷积的核参数不用更新，其实没必要使用复杂的深度学习框架，如果Numpy中可以实现这些功能就更简单方便了。

说干就干，经过查找发现Numpy.convolve可以实现我们想要的功能。

3.Numpy.convolve介绍

numpy.convolve(a, v, mode=‘full’)
参数：
　　　　a:(N,)输入的一维数组
　　　　v:(M,)输入的第二个一维数组
　　　　mode:{‘full’, ‘valid’, ‘same’}参数可选
　　　　　　‘full’　默认值，返回每一个卷积值，长度是N+M-1,在卷积的边缘处，信号不重叠，存在边际效应。
　　　　　　‘same’　返回的数组长度为max(M, N),边际效应依旧存在。
　　　　　　‘valid’ 　返回的数组长度为max(M,N)-min(M,N)+1,此时返回的是完全重叠的点。边缘的点无效。

和一维卷积参数类似，a就是被卷积数据，v是卷积核大小。

4.算法实现

def np_move_avg(a,n,mode="same"):
    return(np.convolve(a, np.ones((n,))/n, mode=mode))

原理说明

运行平均值是卷积数学运算的一个例子。对于运行平均值，沿着输入滑动窗口并计算窗口内容的平均值。对于离散的1D信号，卷积是相同的，除了代替计算任意线性组合的平均值，即将每个元素乘以相应的系数并将结果相加。那些系数，一个用于窗口中的每个位置，有时称为卷积核。现在，N值的算术平均值是(x_1 + x_2 + ... + x_N) / N，所以相应的内核是(1/N, 1/N, ..., 1/N)，这正是我们通过使用得到的np.ones((N,))/N。

边缘处理

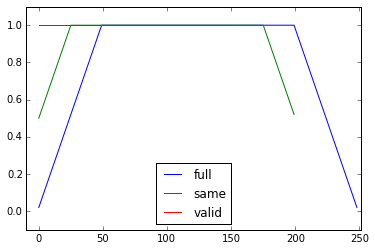
该mode的参数np.convolve指定如何处理边缘。在这里选择了same模式，这样可以保证输出长度一种，但你可能还有其他优先事项。这是一个说明模式之间差异的图：

import numpy as np
import matplotlib.pyplot as plt
 
def np_move_avg(a,n,mode="same"):
    return(np.convolve(a, np.ones((n,))/n, mode=mode))
 
modes = ['full', 'same', 'valid']
for m in modes:
    plt.plot(np_move_avg(np.ones((200,)), 50, mode=m));
 
plt.axis([-10, 251, -.1, 1.1]);
 
plt.legend(modes, loc='lower center');
 
plt.show()

5.参考

1.https://stackoverflow.com/questions/13728392/moving-average-or-running-mean