[Link-Cut-Tree][BZOJ2631]Tree

题面

Description:

一棵\(n\)个点的树，每个点的初始权值为\(1\)。对于这棵树有\(q\)个操作，每个操作为以下四种操作之一：

• + u v c：将\(u\)到\(v\)的路径上的点的权值都加上自然数\(c\)；
• - u1 v1 u2 v2：将树中原有的边\(u1-v1\)删除，加入一条新边\(u2-v2\)，保证操作完之后仍然是一棵树；
• * u v c：将\(u\)到\(v\)的路径上的点的权值都乘上自然数\(c\)；
• / u v：询问\(u\)到\(v\)的路径上的点的权值和，求出答案对于\(51061\)的余数。

Input

第一行两个整数\(n,q\)

接下来\(n-1\)行每行两个正整数\(u,v\)，描述这棵树

接下来\(q\)行，每行描述一个操作

Output

对于每个/对应的答案输出一行

Sample Input

3 2

1 2

2 3

* 1 3 4

/ 1 1

Sample Output

4

HINT

100%的数据保证，$$1\le n,q\le 100000,1\le u,v,u1,v1,u2,v2\le n,0\le c\le 100001$$

Link-cut Tree 的作用&思想

• 作用：类似于动态树链剖分（可以修改点、边）

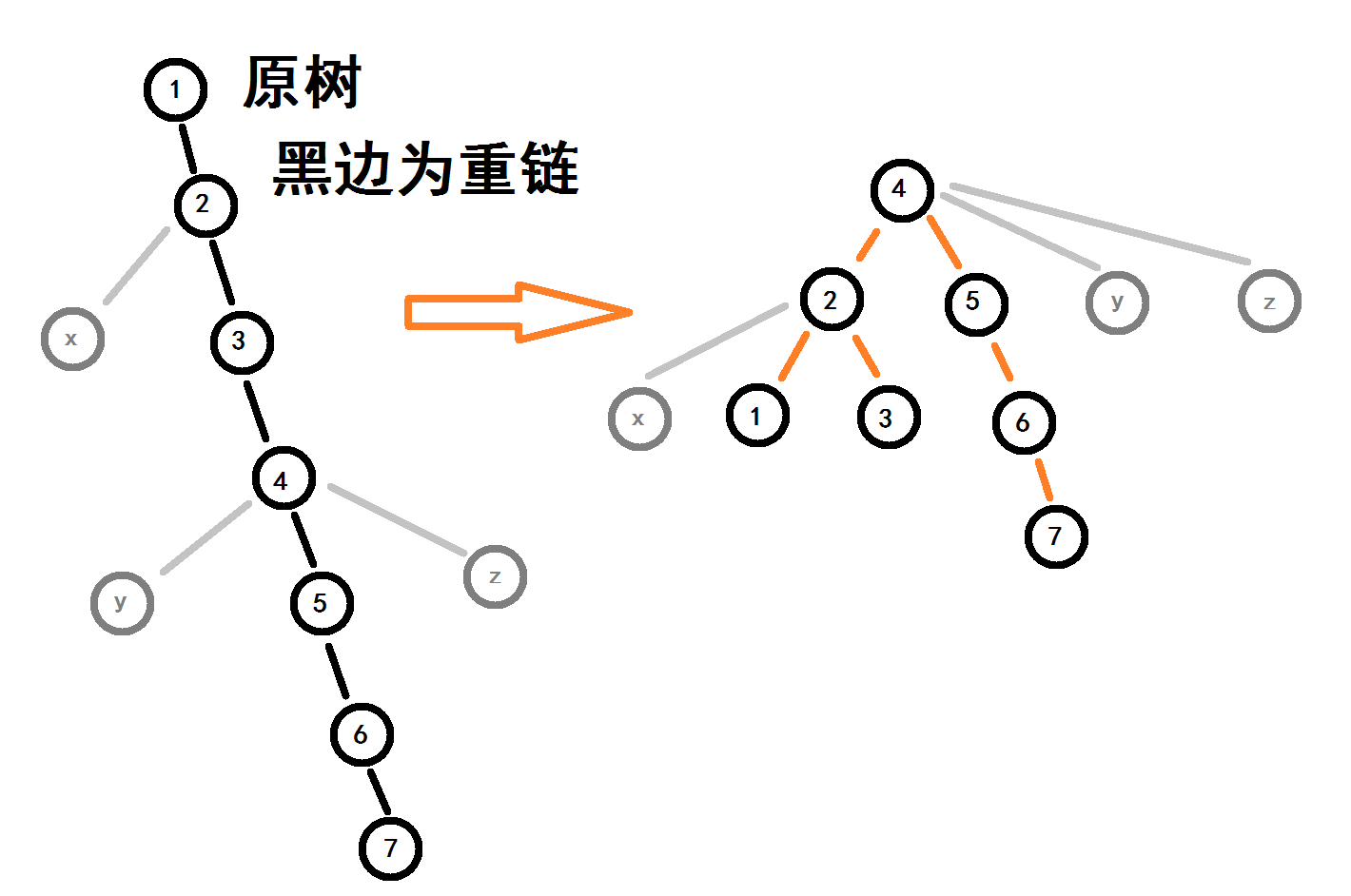
• 思想：用链的思想，把树剖为多个伸展树

  树与树之间只保存父关系，不保存子关系。

树链剖分把树分成若干条重链，对于每条重链，用线段树来维护信息。利用各线段树的信息来得到答案。

Link-cut Tree 的基本操作

1.access(u):把u到根节点变成一条链

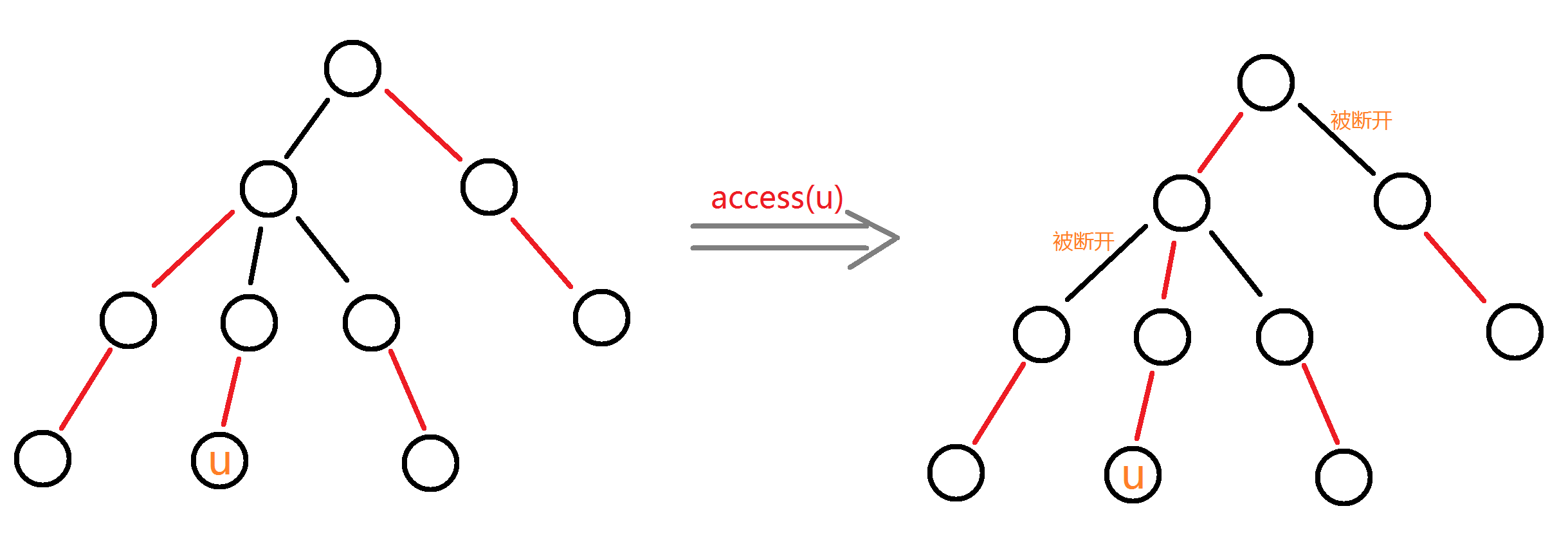
u是当前点，v是前驱

其实就是一层一层往上爬，每次顺带修改链上的儿子

void access(int u){
	for(int v=0;u;v=u,u=fa[u]){
		splay(u);
		ch[u][1]=v;
		pushup(u);
	}
}

2.makeroot(u):把u变成根

access+splay后，u已经是根，可splay的路径上需要进行父子反向，其他的没有影响，因此要进行翻转

void makeroot(int u){
	access(u);
	splay(u);
	reverse(u);
}

3.cut(u,v):切断u,v之间的连接

我们先makeroot(u)+access(v)+splay(v)

由于u和v同在一棵Splay中且u一定是v的父亲，所以Splay中v的左儿子一定是u，断开即可。

void cut(int a,int b){
	makeroot(a);
	access(b);
	splay(b);
	ch[b][0]=0;
	fa[a]=0;
	pushup(b);
}

4.link(u,v):连接u,v

把u变成根，这时u没有父亲，就可以安心连接了。再把其父亲设为v，就实现了连接。

void link(int a,int b){
	makeroot(a);
	fa[a]=b;
}

5.isconnect(u,v):检测u,v是否连接

我们先makeroot(u)+access(v)+splay(v)

如果u和v不在同一棵LCT中，执行makeroot(u)后，u的父亲应该为空(他是根)

除非a和b在同一棵树中，在access(v)+splay(v)后，u与v应该在同一棵Splay中，既然v是根，那么u就不是根，即u一定有一个父亲存在。

bool isconnect(int a,int b){
    if(a==b) return true;
    makeroot(a);
    access(b);
    splay(b);
    return fa[a];
}

---

代码

注意有多个修改中懒标的特殊处理方式。

#include<iostream>
#include<cstdio>
using namespace std;
int ch[100001][2],fa[100001],siz[100001],lazr[100001],cnt,n,q;
unsigned num[100001],tot[100001],lazp[100001],lazc[100001],mod=51061;
inline unsigned rd(){
	unsigned re=0;
	char ch=getchar();
	while(ch<'0'||ch>'9')ch=getchar();
	while(ch>='0'&&ch<='9'){
		re=re*10+ch-'0';
		ch=getchar();
	}
	return re;
}
inline bool isroot(int bt){return ch[fa[bt]][0]!=bt&&ch[fa[bt]][1]!=bt;}
inline int drct(int bt){return ch[fa[bt]][1]==bt;}
inline void pushup(int bt){siz[bt]=siz[ch[bt][0]]+siz[ch[bt][1]]+1;tot[bt]=((tot[ch[bt][0]]+num[bt])%mod+tot[ch[bt][1]])%mod;}
inline void reverse(int bt){swap(ch[bt][0],ch[bt][1]);lazr[bt]^=1;}
inline void add(int bt,unsigned c){num[bt]=(num[bt]+c)%mod;tot[bt]=(tot[bt]+siz[bt]*c)%mod;lazp[bt]=(lazp[bt]+c)%mod;}
inline void times(int bt,unsigned c){num[bt]=(num[bt]*c)%mod;tot[bt]=(tot[bt]*c)%mod;lazc[bt]=(lazc[bt]*c)%mod;lazp[bt]=(lazp[bt]*c)%mod;}
inline void pd(int bt){
	if(lazr[bt]){
		if(ch[bt][0])reverse(ch[bt][0]);
		if(ch[bt][1])reverse(ch[bt][1]);
		lazr[bt]=0;
	}
	if(lazp[bt]){
		if(ch[bt][0])add(ch[bt][0],lazp[bt]);
		if(ch[bt][1])add(ch[bt][1],lazp[bt]);
		lazp[bt]=0;
	}
	if(lazc[bt]!=1){
		if(ch[bt][0])times(ch[bt][0],lazc[bt]);
		if(ch[bt][1])times(ch[bt][1],lazc[bt]);
		lazc[bt]=1;
	}
}
inline void pushdown(int u){
	if(!isroot(u))pushdown(fa[u]);
	pd(u);
}
inline void rotate(int u){
	int f=fa[u],g=fa[f],c=drct(u);
	if(!isroot(f))ch[g][drct(f)]=u;
	fa[u]=g;
	ch[f][c]=ch[u][c^1];
	if(ch[f][c])fa[ch[f][c]]=f;
	ch[u][c^1]=f;
	fa[f]=u;
	pushup(f);
	pushup(u);
}
void splay(int u){
	pushdown(u);
	while(!isroot(u)){
		if(!isroot(fa[u]))rotate(drct(fa[u])==drct(u)?fa[u]:u);
		rotate(u);
	}
}
void access(int u){
	for(int v=0;u;v=u,u=fa[u]){
		splay(u);
		ch[u][1]=v;
		pushup(u);
	}
}
void makeroot(int u){
	access(u);
	splay(u);
	reverse(u);
}
void link(int a,int b){
	makeroot(a);
	fa[a]=b;
}
void cut(int a,int b){
	makeroot(a);
	access(b);
	splay(b);
	ch[b][0]=0;
	fa[a]=0;
	pushup(b);
}
void makeline(int u,int v){
	makeroot(u);
	access(v);
	splay(v);
}
int main(){
	n=rd();
	q=rd();
	for(int i=1;i<=n;i++)lazc[i]=num[i]=tot[i]=siz[i]=1;
	for(int i=1;i<n;i++){
		int u=rd(),v=rd();
		link(u,v);
	}
	makeroot(1);
	for(int i=1;i<=q;i++){
		char cha[5];
		scanf("%s",cha);
		int u=rd(),v=rd();
		if(cha[0]=='+'){
			unsigned c=rd();
			makeline(u,v);
			add(v,c);
		}else if(cha[0]=='-'){
			int u2=rd(),v2=rd();
			cut(u,v);
			link(u2,v2);
		}else if(cha[0]=='*'){
			unsigned c=rd();
			makeline(u,v);
			times(v,c);
		}else if(cha[0]=='/'){
			makeline(u,v);
			printf("%u\n",tot[v]);
		}
	}
}