2020-2021-1 20209307 《Linux内核原理与分析》第九周作业

这个作业属于哪个课程	<2020-2021-1Linux内核原理与分析）>
这个作业要求在哪里	<2020-2021-1Linux内核原理与分析第九周作业>
这个作业的目标	<进程的切换与系统的一般执行过程>
作业正文	https://www.cnblogs.com/wzyxiaowang/p/14091796.html

一、知识点

1、硬中断和软中断

硬中断：由与系统相连的外设(比如网卡、硬盘)自动产生的。主要是用来通知操作系统系统外设状态的变化。比如当网卡收到数据包的时候，就会发出一个中断。我们通常所说的中断指的是硬中断(hardirq)。

软中断：为了满足实时系统的要求，中断处理应该是越快越好。linux为了实现这个特点，当中断发生的时候，硬中断处理那些短时间就可以完成的工作，而将那些处理事件比较长的工作，放到中断之后来完成，也就是软中断(softirq)来完成。

异常：故障（Fault）：出现问题，可以恢复到当前指令。

退出（Abort）：不可恢复的严重故障，导致程序无法继续运行，只能退出。

陷阱（Trap）：程序主动产生的异常。

2、进程调度时机

中断处理过程（包括时钟中断、I/O中断、系统调用和异常）中，直接调用schedule()，或者返回用户态时根据need_resched标记调用schedule()；

内核线程可以直接调用schedule()进行进程切换，也可以在中断处理过程中进行调度，也就是说内核线程作为一类的特殊的进程可以主动调度，也可以被动调度；

用户态进程无法实现主动调度，仅能通过陷入内核态后的某个时机点进行调度，即在中断处理过程中进行调度。

3、Linux系统进程调度与进程切换过程的理解

进程调度的时机：

中断处理过程（包括时钟中断、I/O中断、系统调用和异常）中，直接调用schedule()，或者返回用户态时根据need_resched标记调用schedule()；比如sleep，就可能直接调用了schedule

内核线程可以直接调用schedule()进行进程切换，也可以在中断处理过程中进行调度，也就是说内核线程作为一类的特殊的进程可以主动调度，也可以被动调度；

用户态进程无法实现主动调度，仅能通过陷入内核态后的某个时机点进行调度，即在中断处理过程中进行调度。用户态进程只能被动调度。

进程的切换：

为了控制进程的执行，内核必须有能力挂起正在CPU上执行的进程，并恢复以前挂起的某个进程的执行，这叫做进程切换、任务切换、上下文切换；即进程上下文切换

挂起正在CPU上执行的进程，与中断时保存现场是不同的，中断前后是在同一个进程上下文中，只是由用户态转向内核态执行；

进程上下文包含了进程执行需要的所有信息

用户地址空间：包括程序代码，数据，用户堆栈等

控制信息：进程描述符，内核堆栈等

硬件上下文（注意中断也要保存硬件上下文只是保存的方法不同）

schedule()函数选择一个新的进程来运行，并调用context_switch进行上下文的切换，这个宏调用switch_to来进行关键上下文切换

next = pick_next_task(rq, prev);//进程调度算法都封装这个函数内部

context_switch(rq, prev, next);//进程上下文切换

switch_to利用了prev和next两个参数：prev指向当前进程，next指向被调度的进程

二、实验八：理解进程调度时机跟踪分析进程调度与进程切换的过程

1、配置运行MenuOS系统

2、启动gdb，在schedule、context_switch、pick_next_task设置断点、使用c继续运行

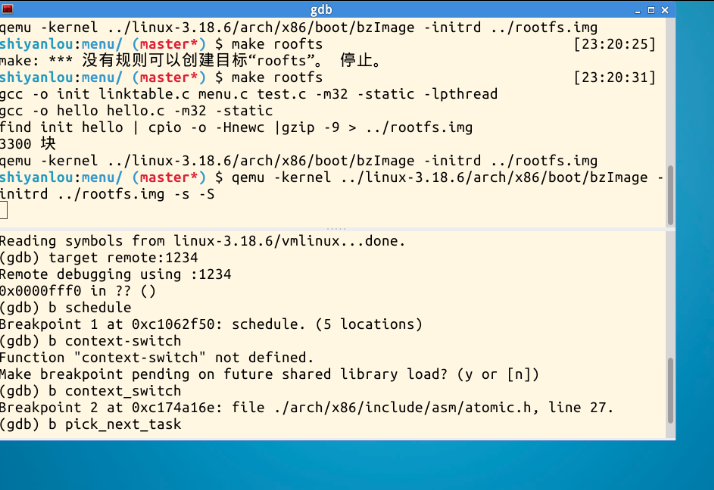
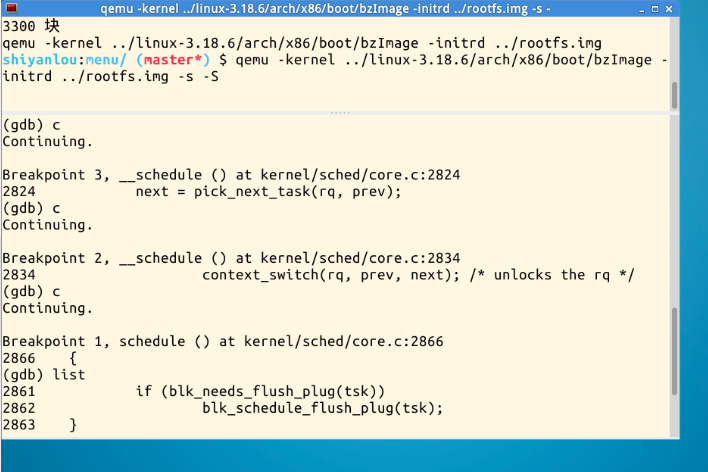
3、使用list查看断点处代码

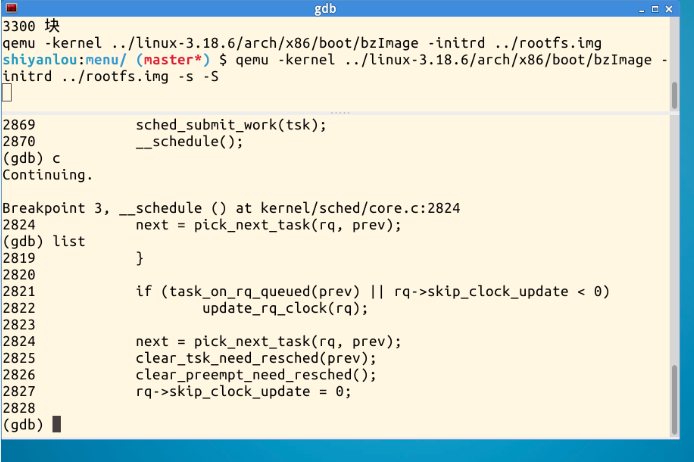
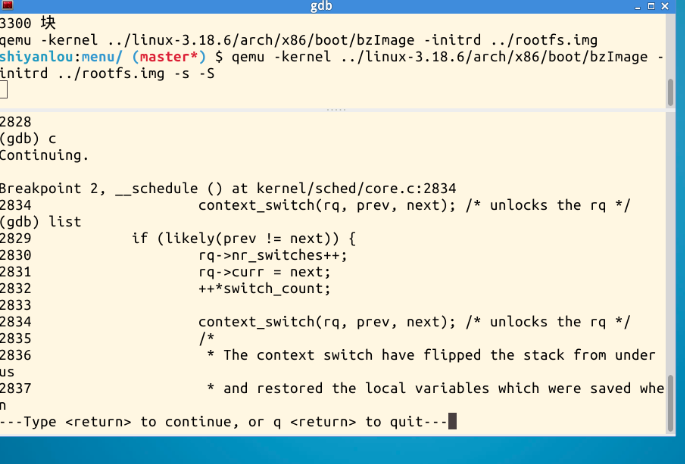
三、总结

Linux内核中实现进程的切换主要通过保存进程相关的信息实现，这里需要注意进程切换中内核级进程的切换和用户态进程切换的不同。进程调度是为了合理分配计算机资源，并让每个进程都获得适当的执行机会。由于进程调度函数schedule是内核态函数，且并非系统调用，故用户态进程只能在发生中断时被动地调度。