P1433 吃奶酪（洛谷）状压dp解法

嗯？这题竟然是个绿题。

这个题真的不（很）难，我们只是不会计算2点之间的距离，他还给出了公式，这个就有点……

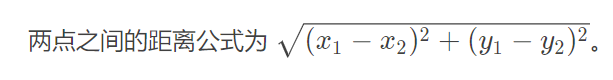
我们直接套公式去求出需要的值，然后普通的状压dp就可以了。

是的状压dp。

这个题的数据加强了，早已经不是搜索可以驾驭的了。

搜索的效率实在是有点低，我来算一个不准的效率，搜索的效率应该是O(n!)。应该是吧。

状压dp只需要短短的O(2^n*n*n就可以了)。状态共有2^n*n个，每次查找下一步需要O(n)的效率，所以状压dp的效率是O(2^n*n*n)。

状压dp用一个二进制数表示哪个奶酪曾经吃过，我们先看看这些二进制数的基本操作：不知道与，或，异或运算的可以百度一下。

第一种操作，查询第i个奶酪有没有吃过。

x表示现在奶酪的情况（2进制数）

我们要判断第i个奶酪有没有被吃

if((x&(1<<i-1))==0)

这样写就可以啦。其中&的意思是按位与运算，就是说在2进制下，2位同时为1，结果才为1，也就是说，如果第i个奶酪被吃掉了，x那一位就是1，按位与运算后的结果也是1，如果按位与运算后的结果是0，第i个奶酪就没有被吃掉。

第二种操作，吃掉第i个奶酪后，x会变成什么样子？

x=x|(1<<i-1)

这样写，|是按位或运算，就是在二进制里，2位有一个为1，结果为1，1<<i-1的第i位是1，和x进行按位或运算就让x的第i位也变成1了。

做这个题只需要这两个操作，剩下的操作有兴趣的同学可以去百度一下。

接下来就是代码了：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<cstdio>
using namespace std;
double a[20],b[20],shu=999999.0;//初始化
double dp[40000][20];
double sz[20][20];//sz[i][j]是表示第i个奶酪到第j个奶酪有多远。
long long n;
int main()
{
	scanf("%lld",&n);
	for(int i=0;i<(1<<n);i++)
	{
		for(int j=1;j<=n;j++)
		{
			dp[i][j]=999999.0;//还是初始化
		}
	}
	for(int i=1;i<=n;i++)
	{
		cin>>a[i]>>b[i];
	}
	a[0]=0;//依然是初始化
	b[0]=0;//因为老鼠一开始在0，0的位置。
	for(int i=0;i<=n;i++)
	{
		for(int j=0;j<=n;j++)
		{
			sz[i][j]=sqrt((a[i]-a[j])*(a[i]-a[j])+(b[i]-b[j])*(b[i]-b[j]));//公式摆着呢，题目给了。
		}
	}
	for(int i=1;i<=n;i++)//1<<i-1是把1左移i-1位，在二进制就是第i位是1。dp[i][j]中的i表示现在的情况（二进制数），j表示现在在哪个奶酪哪里。dp[i][j]的值就是达成这个局势最少走多远。
	{
		dp[1<<i-1][i]=sz[0][i];
	}
	for(int i=1;i<=(1<<n)-1;i++)//所有情况，也就是n个1，也就是(1<<n)-1。
	{
		for(int j=1;j<=n;j++)//在第j个奶酪处。
		{
			if(dp[i][j]!=999999)//这种情况不可能，比如i=1,j=2;
			{
				for(int k=1;k<=n;k++)//他的起始点出现过，搜索还能走到哪个奶酪处。
				{
					if((i&(1<<k-1))==0)//这个奶酪处没来过。
					{
						dp[i|(1<<k-1)][k]=min(dp[i|(1<<k-1)][k],dp[i][j]+sz[j][k]);//来这个奶酪处。判断一下这样走是不是最近的。
					}//有2种可能，第一，之前来过，而且走的距离比这次小，第二种，这次走的距离加上目前位置到第k个奶酪的距离是最短的。反正我们直接找最短的就好。
				}
			}
		}
	}
	for(int i=1;i<=(1<<n)-1;i++)
	{
		for(int j=1;j<=n;j++)
		{
			if(i==(1<<n)-1)
			{
				shu=min(shu,dp[i][j]);//这里为了方便查找错误写的，可以更优化一点，但没必要。
			}
		}
	}
	printf("%.2f",shu);//输出。
	return 0;
}

好了，这个题目就这么愉快的讲完了。