GC算法介绍及工作原理和优缺点

一.GC定义与作用

GC就是垃圾回收机制的简写 GC可以找到内存中的垃圾，并释放和回收空间，GC里的垃圾是什么 如下图所示：

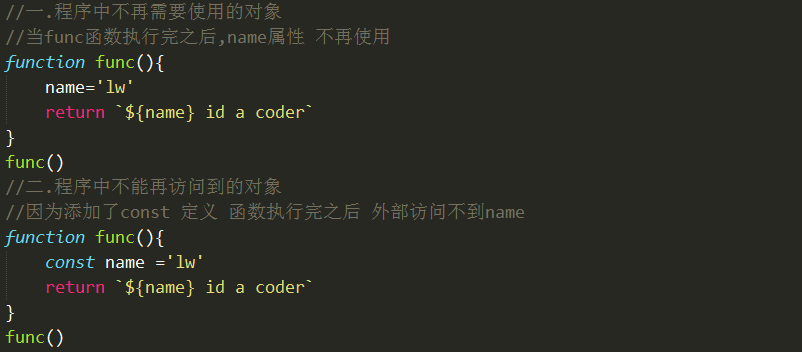
GC算法是什么：GC是一种机制,垃圾回收器完成具体的工作 工作的内容就是查找垃圾释放空间,回收空间算法就是工作时查找和回收

所遵循的规则。常见GC算法有引用计数，标记清除，标记整理，分代回收。

二.GC算法的工作原理及优缺点

1.引用计数算法实现原理

核心思想：设置引用数，判断当前引用数是否为0 引用关系改变时修改引用数字，比如有一个对象指向它 他的引用计数+1 多个对象

引用,引用计数累加引用计数累加，当没有对象引用时引用计数为0 GC立即进行回收，下面通过代码来分析下工作原理：

上述代码中,从全局角度出发，user1,user2及meauList 计数都不为0 ，num1和num2，当函数fn()执行完成后全局作用访问不到num1

和num2，所以说num1和num2计数为0，会被GC回收。当所有的代码执行完成后，user1和user2也不为0，因为被meauList数组中引

用，所以计数+1

2.引用计数算法的优缺点

优点:

最大限度的减少程序暂停，内存有一定的上限，当内存即将爆满时，引用计数会立马找到数值为0的计数空间对其进行释放，这样就保

证了内存不会有暂满的时候。

缺点:

1.时刻监听着引用数值是否需要修改，时间开销比较大

2.无法回收循环引用的对象 具体用代码实现如下图所示：

如上图所示：当fn执行完成后,obj1和obj2都是局部变量，按说是要被回收的,但是后面obj1.name=obj2，obj2.name=obj1有着互相被

引用的关系，所以说数值并不为0，就没有办法对这两个空间进行回收了，从而造成了内存空间的浪费，这也就是对象之间的循环引

用。

3.标记清除算法实现原理

核心思想：分标记和清除 二个阶段完成，

第一个阶段 遍历所有对象找标记活动对象(可达对象)。

第二个阶段 把那些没有被标记的对象进行清除 同时也会抹掉第一个阶段的标记 便于我们GC下次正常的工作把回收的空间放到一个

空闲列表的上面,方便我们的程序后续直接在这里申请空间。

用图示方式进行举例说明:

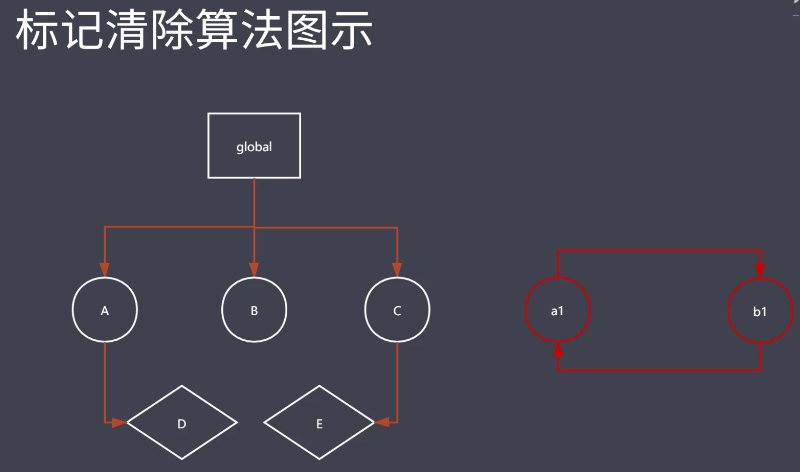
如上图所示A B C为全局变量,D E被A和C引用 所以ABCDE都是可达对象 第一步会被标记上，第二阶段 查询没有被标记的对象 如上

图中的a1和b1为未标记的,全局作用域内查询不到,则会被GC清除掉。

4.标记清除算法的优缺点

优点：

可以回收循环引用的对象,如上图所示,比如a1和b1为函数内部的局部变量,就失去了与全局global的连接，不可达的对象在标记阶段就

不可标记，在第二个阶段会被清除，而在引用计数算法中有引用的关系 所以计数不为0 所以不能被清除

缺点：

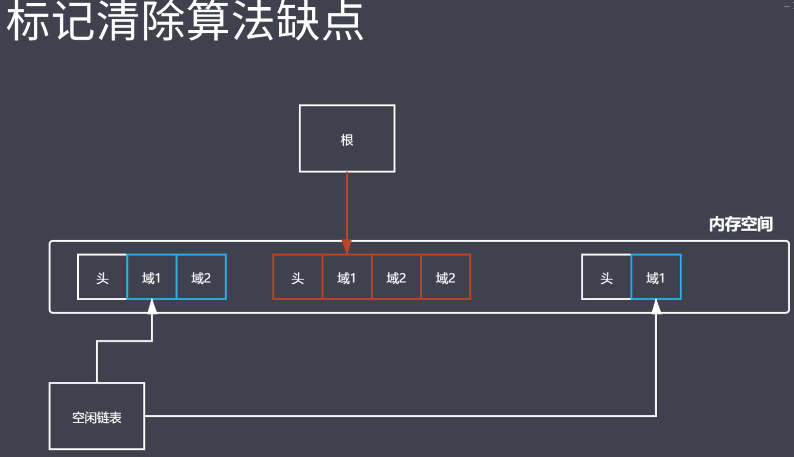
如下图所示，我们从根去查找 红色区域为一个可达对象，左右两侧分别为两个不可达的对象，在第二轮的清除操作中会被清除掉，再

把剩余空间添加到空闲列表之上，这就有一个问题了，比如最左侧的是B对象，中间的可达对象为A对象，最右侧的为C对象，BC对象

存储语言信息，比如大小和地址，我们称之为头。还有一个我们存放数据的称之为域，看上去是释放了3个域的大小，但是中间间隔着

A对象，其实他们还是分散的，也就是地址不连续，如果说操那个申请列表申请1.5个域大小的空间，左侧超出了浪费，右侧直接就不够

，称之为空间的碎片化。

5.标记整理算法的实现原理

标记整理可以看做标记清除的一个增强操作，标记阶段的操作与标记清除一致，第二个阶段在标记清除阶段会先执行整理，移动对

象位置，这样可以避免分散的地址的不连续的小空间，如下图所示：