题解-CF1307G Cow and Exercise

CF1307G Cow and Exercise

给 \(n\) 点 \(m\) 边的带权有向图，边 \(i\) 为 \((u_i,v_i,w_i)\)。\(q\) 次询问，每次给 \(x_i\)，问修改一些边使整张图的边权和增加 \(x_i\) 后最短路最大值（可以把边权修改为浮点数）。

数据范围：\(2\le n\le 50\)，\(1\le m\le n\cdot (n-1)\)，\(1\le u_i,v_i\le n\)，\(1\le w_i\le 10^6\)，\(1\le q\le 10^5\)，\(0\le x_i\le 10^5\)。

---

学网络流不能错过的经典例题啊！这题的思想真是又巧妙又易懂又实用。

我写的题解如下，貌似废话很多。。。

---

如下图：

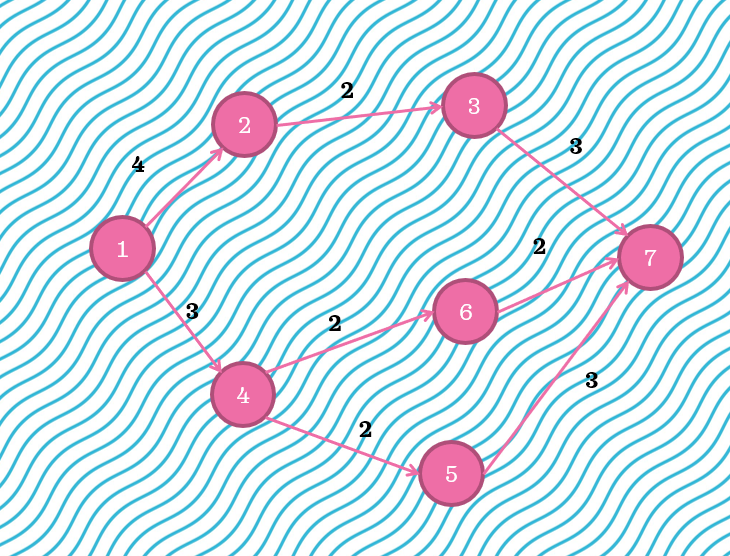
如果 \(x=0\)，最短路最长为 \(7\)。

如果 \(x=1\)，最短路最长为 \(8\)。\((1,4,3)\to(1,4,4)\)。

如果 \(x=2\)，最短路最长为 \(9\)。\((1,4,3)\to(1,4,5)\)。

如果 \(x=3\)，最短路最长为 \(9.5\)。\((1,4,3)\to(1,4,5.5)\)，\((1,2,4)\to(1,2,4.5)\)。

如果 \(x=4\)，最短路最长为 \(10\)。\((1,4,3)\to(1,4,6)\)，\((1,2,4)\to(1,2,5)\)。

\(\cdots\)

直到 \(x=\infty\)，都只需要改 \((1,4,3)\) 和 \((1,2,4)\) 两条边。

因为它们是图中三条路径的必经之路。

学过的人应该可以发现：它们便是无权图上的最小割边。

要使带权图最短路最长，修改最小割边是最优的。

将经过同一个最小割边的路径归为一个路径集。

如上图中，设经过 \((1,2,4)\) 的路径集为 \(S_1\)，经过 \((1,4,3)\) 的路径集为 \(S_2\)。

当 \(0\le x\le 2\) 时，只需修改 \(S_2\) 的割边 \((1,4,3)\)。

当 \(3\le x\) 时，需要修改 \(S_1\) 和 \(S_2\) 的割边，并要使两个路径集的最短路径相等。

类推一下，根据平均的思想，可以得出：

1. 无论 \(x\) 取何值，修改最短路径长度最短的 \(k\) 个路径集，并使它们修改后相等是最优的。

2. 假设这 \(k\) 个路径集修改后的最短路径都为 \(L\)，则应有对于任何未被修改割边的路径集，最短路径长度 \(\ge L\)。否则去修改这条路径必然更优。

---

所以就可以让费用流算法上路了，这题建议用 \(\tt EK\)，因为这东西很乖的，一次就增广一个路径集。

回想一下 \(\tt EK\) 的套路：\(\tt Spfa\) 找到最短路，然后增广。

如果让网络流的边 \(flow_i=1,cost_i=w_i\)，则有：

增广 \(k\) 次后，当前的 \(flow=k\)，并且当前的 \(cost\) 为 \(k\) 个路径集的最短路长度和。

所以可以把每次增广后的 \(flow\) 和 \(cost\) 扔进 \(\tt vector\) 里。

然后对于每个询问，\(Res=\min\{\frac{cost_j+x}{flow_j}\}\)。

---

这时有个问题：要是 \(j\) 不等于最优的 \(k\) 怎么办？

有个很神奇的结论：对于 \(j=k\) 的情况，\(\frac{cost_j+x}{flow_j}\) 最小。

根据上面的结论，如果 \(j>k\)，因为把最短路径更长的路径集也考虑进来了，所以 \(\frac{cost_j+x}{flow_j}>\frac{cost_k+x}{flow_k}\)。

如果 \(j<k\)，那么修改完后这 \(j\) 个路径集的最短路径会 \(>\) 剩下未被修改的 \(k-j\) 个路径集，所以也可得这结论。

---

时间复杂度 \(\Theta(n^4+nq)\)。

---

• 代码

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=50;
int n,m,q;
vector<pair<int,int>> fc;

//EK
int fn,s,t;
vector<int> e[N+7],to,fw,co;
void add(int u,int v,int f,int c){
	e[u].pb(sz(to)),to.pb(v),fw.pb(f),co.pb(+c);
	e[v].pb(sz(to)),to.pb(u),fw.pb(0),co.pb(-c);
}
int dep[N+7],p[N+7],vis[N+7];
int Bfs(){
	for(int i=1;i<=fn;i++) dep[i]=inf,vis[i]=0;
	queue<int> q; q.push(s),vis[s]=1,dep[s]=0;
	while(sz(q)){
		int u=q.front(); q.pop(),vis[u]=0;
		for(int&v:e[u])if(fw[v]&&dep[to[v]]>dep[u]+co[v]){
			dep[to[v]]=dep[u]+co[v],p[to[v]]=v;
			if(!vis[to[v]]) vis[to[v]]=1,q.push(to[v]);
		}
	}
	return dep[t]<inf;
}
int flow,cost;
void EK(){
	while(Bfs()){
		int f=inf;
		for(int i=t;i!=s;i=to[p[i]^1]) f=min(f,fw[p[i]]);
		flow+=f,cost+=dep[t]*f;
		for(int i=t;i!=s;i=to[p[i]^1]) fw[p[i]]-=f,fw[p[i]^1]+=f;
		fc.pb(mp(flow,cost));
	}
}

//Main
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,u,v,w;i<=m;i++)
		scanf("%d%d%d",&u,&v,&w),add(u,v,1,w);
	s=1,t=fn=n,EK();
	scanf("%d",&q);
	for(int i=1,x;i<=q;i++){
		scanf("%d",&x);
		db res=inf;
		for(auto d:fc) res=min(res,db(d.y+x)/d.x);
		printf("%.10lf\n",res);
	}
	return 0;
}

---

祝大家学习愉快！