P2561 [AHOI2002]黑白瓷砖

$ \color{#0066ff}{ 题目描述 }$

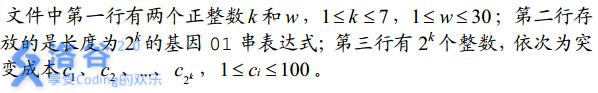
\(\color{#0066ff}{输入格式}\)

文件中以一行的形式存放一个正整数 n ， n ≤ 20 。

\(\color{#0066ff}{输出格式}\)

以一行的形式输出问题的解 s (解的位数不超过 200 位)。

\(\color{#0066ff}{输入样例}\)

1

2

\(\color{#0066ff}{输出样例}\)

2

4

\(\color{#0066ff}{数据范围与提示}\)

none

\(\color{#0066ff}{题解}\)

显然直接上Polya

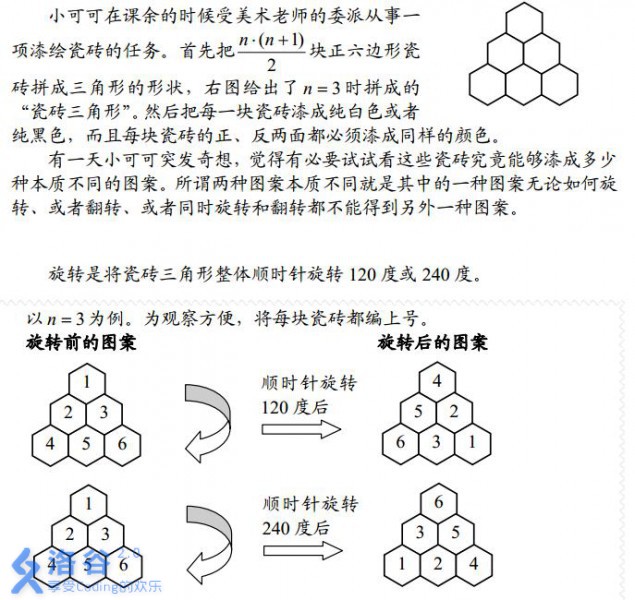
不难发现有6种置换

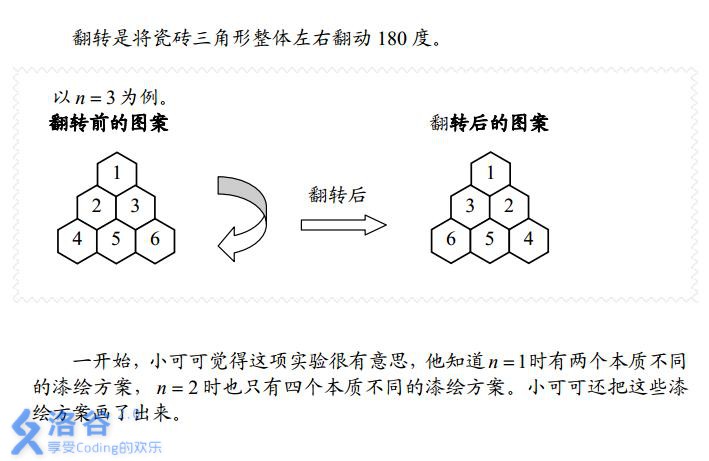
旋转0,120,240度，还有三种对称轴的翻转

(以下图片均来自--------lzxkj)

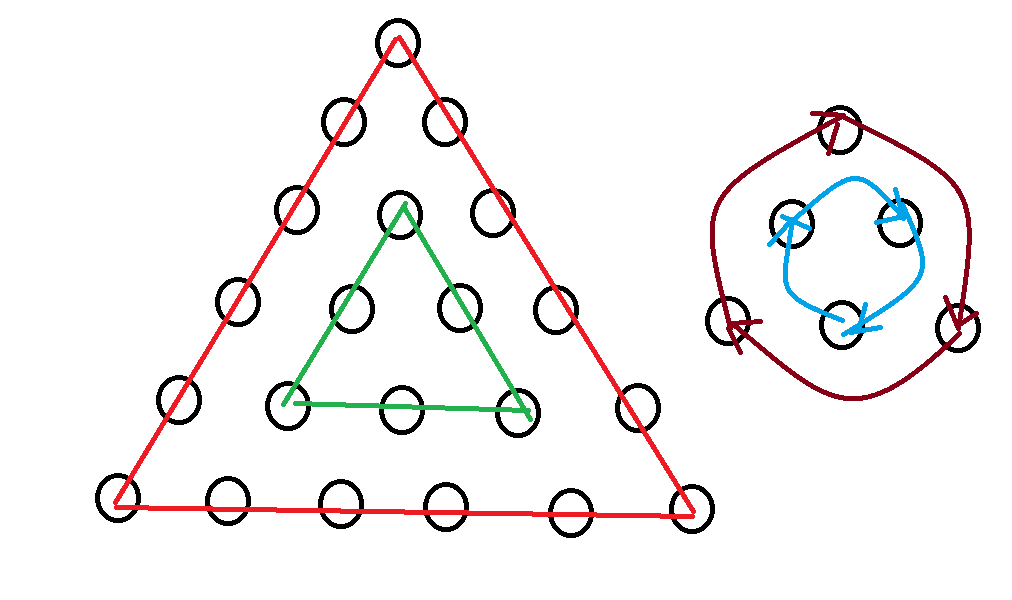
对于旋转来说，肯定是三个一循环，但是会存在下面的情况

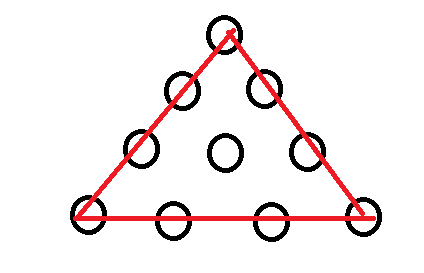
所以答案就是\(x=\lceil \frac {\frac {n*(n+1)}{2}}{3}\rceil=\lceil \frac {n*(n+1)}{6}\rceil\)

注意，旋转0度是\(y=\frac{n*(n + 1)}{2}\)

翻转，中间对称的不变，总共\(\lceil \frac n 2 \rceil\)个，于是方案为\(z=\frac{\frac{n*(n+1)}{2}-\lceil \frac{n}{2}\rceil}{2}+\lceil \frac{n}{2}\rceil=\frac{1}{2}(\frac{n*(n+1)}{2}+\lceil \frac{n}{2}\rceil)\)

因此\(ans=\frac{2^y+2*2^x+3*2^z}{6}\)

显然并没有取模

直接上Python！

import math
n = int(input())
tot = n * (n + 1) >> 1;
x = tot
y = math.ceil(n * (n + 1) / 6)
z = (tot + math.ceil(n / 2)) >> 1;
ans = (2 ** x + 2 * 2 ** y + 3 * 2 ** z) // 6;
print(ans)