ACM-ICPC 2018 徐州赛区网络预赛 A.Hard to prepare 【规律递推】

任意门：https://nanti.jisuanke.com/t/31453

A.Hard to prepare

After Incident, a feast is usually held in Hakurei Shrine. This time Reimu asked Kokoro to deliver a Nogaku show during the feast. To enjoy the show, every audience has to wear a Nogaku mask, and seat around as a circle.

There are N guests Reimu serves. Kokoro has 2^k2k masks numbered from 0,1,\cdots,0,1,⋯, 2^k - 12k−1, and every guest wears one of the masks. The masks have dark power of Dark Nogaku, and to prevent guests from being hurt by the power, two guests seating aside must ensure that if their masks are numbered ii and jj , then ii XNOR jj must be positive. (two guests can wear the same mask). XNOR means ~(ii^jj) and every number has kk bits. (11 XNOR 1 = 11=1, 00 XNOR 0 = 10=1, 11 XNOR 0 = 00=0)

You may have seen 《A Summer Day's dream》, a doujin Animation of Touhou Project. Things go like the anime, Suika activated her ability, and the feast will loop for infinite times. This really troubles Reimu: to not make her customers feel bored, she must prepare enough numbers of different Nogaku scenes. Reimu find that each time the same guest will seat on the same seat, and She just have to prepare a new scene for a specific mask distribution. Two distribution plans are considered different, if any guest wears different masks.

In order to save faiths for Shrine, Reimu have to calculate that to make guests not bored, how many different Nogaku scenes does Reimu and Kokoro have to prepare. Due to the number may be too large, Reimu only want to get the answer modules 1e9+71e9+7 . Reimu did never attend Terakoya, so she doesn't know how to calculate in module. So Reimu wishes you to help her figure out the answer, and she promises that after you succeed she will give you a balloon as a gift.

Input

First line one number TT , the number of testcases; (T \le 20)(T≤20) .

Next TT lines each contains two numbers, NN and k(0<N, k \le 1e6)k(0<N,k≤1e6) .

Output

For each testcase output one line with a single number of scenes Reimu and Kokoro have to prepare, the answer modules 1e9+71e9+7 .

样例输入复制

2
3 1
4 2

样例输出复制

2
84

题意概括：

有 N 个客人 2^K 顶帽子， 每顶帽子编号为 1 ~ 2^K， N 个客人围成一个圈， 要求相邻两个客人的帽子编号（K位二进制）同或不为0。

解题思路：

第一步：推可能存在的方案数， 这个举几个栗子就可以发现两个帽子不满足条件的情况只有一种，那就是相邻编号互为取反数（二进制取反）。

第二步：

找规律找递推关系。

画一下样例图解会发现 排除 第 1 个 和 第 N 个互为取反数的情况，因为后一个只有一个编号不满足条件的， 所以可能性有 2^K * (2^K-1) ^ ( N-2 ) * (2^K-2);

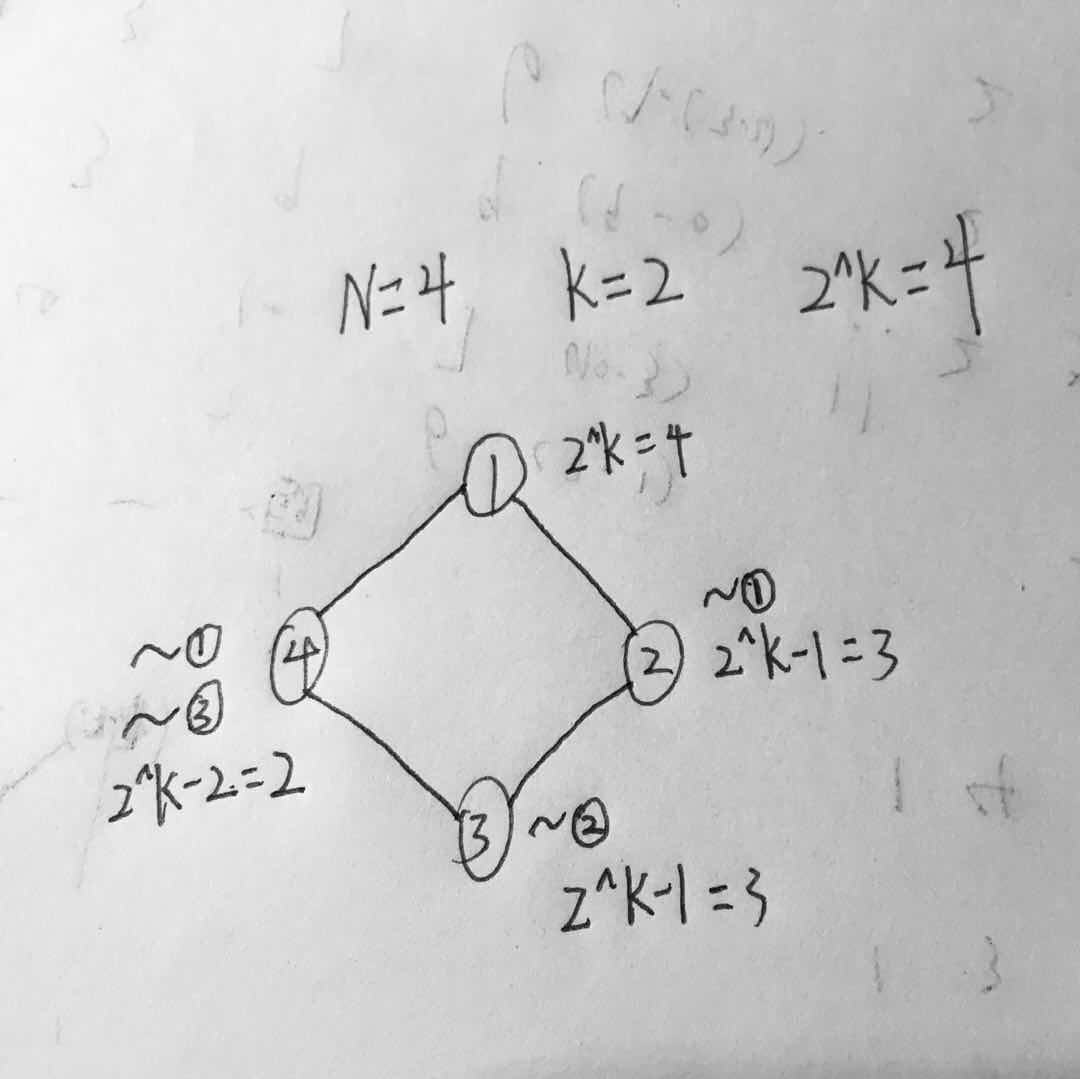
很明显这种情况是不完整的，因为有 ~① == ~③ 的情况。

所以我们接下来要做的就是找到 ~① == ~③ 的情况有多少（也就是① == ③的情况啦）

把这部分漏的补上去就是完整的结果了。

这部分漏的怎么找呢，递推回 N-2 个 按照之前那条规律计算 （ 2^K * (2^K-1) ^ ( N-2-2 ) * (2^K-2);）

然后可能又出现上述情况，继续递推回去，一直算算算...算到只有两个客户或者一个客户的时候就可以停止啦

Tip：

当然这道题也可以先算出  2^K * (2^K-1) ^ ( N-3 ) ；

然后这部分没有考虑  ① ！= ③ 的情况， 所以我们找出 ① ！= ③ 这种情况有多少种。

用总的减去这部分不满足条件的也是答案。

参考：https://blog.csdn.net/qq_36424540/article/details/82586694

我们假设有  颗珠子，   我们不考虑开头 对末尾的限制， 只是考虑  对 的限制，答案就是 ， 这些情况是多了的，多了   这种情况， 然后我们再来计算这种情况有多少？

现在的条件 是 已知 第一个是 ， 最后一个是， 问一共有多少种方案。

我们先考虑简单的情况 ，假设一共只有 3个 珠子  ，我们第一个是A，第三个是， 那么第二个只能选 个。 所以多了的就是 中情况。

然后推广一下， 我们考虑   这个位置是 ，那么   这个位置 只有    种情况， 所以我们减掉  种情况，可是这个情况仍然 少了   这个位置上 是 的情况，所以我们还得加上 现在确定 第一个位置是  A ，第  个位置是  的情况， 所以一直 .......   , 结束的位置在哪里呢？

结束的位置也就是 最早出现 的位置，也就是  第三个位置，所以 我们可以变得位置计算到 第二个也就是  可以了

AC code（第一种）：

 #include <bits/stdc++.h>
 #define INF 0x3f3f3f3f
 #define LL long long
 #define mod 1000000007
 using namespace std;
 const int MAXN = 1e6+;
 LL a[MAXN];
 LL N, K;

 LL pow(LL x, LL n)    //快速幂
 {
     LL res = ;
     while(n){
         if(n&) res = res*x%mod;
         x = x*x%mod;
         n >>= ;
     }
     return res;
 }

 void init()                //初始化求2^k
 {
     a[] = ;
     for(int i = ; i < MAXN; i++)
         a[i] = (a[i-]*2LL)%mod;
 }

 LL check(LL n, LL k)       //递推求解
 {
     if(n == ) return a[k]%mod;
     else if(n == ) return (a[k]*(a[k]-))%mod;
     LL res;
     res = ( (a[k]*pow((a[k]-), n-)%mod) * (max(a[k]-2LL, 0LL)))%mod;
     res = ( res + check(n-, k)%mod)%mod;
     return res;
 }

 int main()
 {
     int T_case;
     init();
     scanf("%d", &T_case);
     while(T_case--){
         scanf("%lld%lld", &N, &K);
         printf("%lld\n", check(N, K));
     }
     return ;
 }