P4320 道路相遇

[Luogu4320]

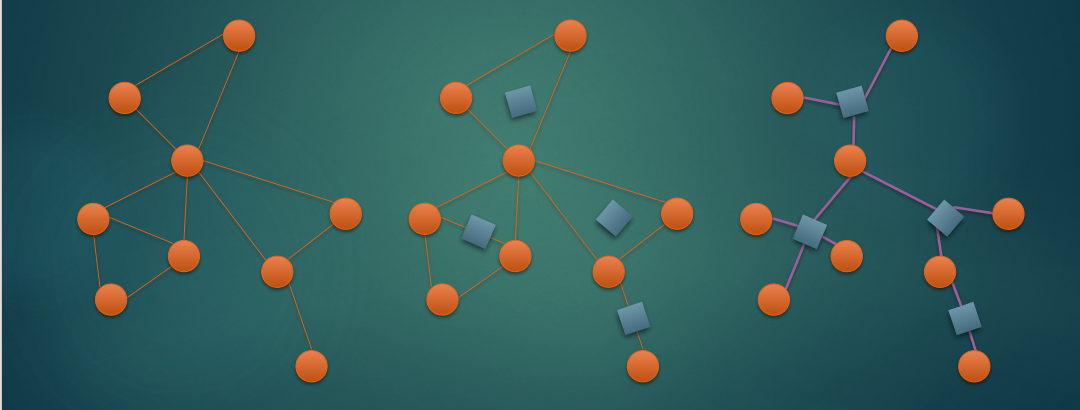
必经点数==圆方树上两点路径上圆点数

也就等于边数/2+1

没什么好说的 , 看代码

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define Debug(x) cout<<#x<<"="<<x<<endl
using namespace std;
typedef long long LL;
const int INF=1e9+7;
inline LL read(){
    register LL x=0,f=1;register char c=getchar();
    while(c<48||c>57){if(c=='-')f=-1;c=getchar();}
    while(c>=48&&c<=57)x=(x<<3)+(x<<1)+(c&15),c=getchar();
    return f*x;
}
const int N=1e6+5;
const int M=2e6+5;
struct Graph{
    struct Edge{
        int v,nxt;
    }e[M];
    int first[N],Ecnt=0;
    inline void Add_edge(int u,int v){
        e[++Ecnt]=(Edge){v,first[u]};
        first[u]=Ecnt;
    }
    inline void link(int u,int v){
        Add_edge(u,v);
        Add_edge(v,u);
    }
}G,T;
int low[N],dfn[N],st[N],size[N],fa[N],top[N],son[N],dep[N];
int n,m,Q,dft,tp;
inline void tarjan(int u){
    dfn[u]=low[u]=++dft;
    st[++tp]=u;
    for(int i=G.first[u];i;i=G.e[i].nxt){
        int v=G.e[i].v;
        if(!dfn[v]){
            tarjan(v);
            low[u]=min(low[u],low[v]);
            if(low[v]>=dfn[u]){
                T.link(++n,u);
                while(st[tp]!=v) T.link(n,st[tp--]);
                T.link(n,st[tp--]);
            }
        }
        else low[u]=min(low[u],dfn[v]);
    }
}
inline void dfs1(int u,int pre){
    dep[u]=dep[pre]+1,fa[u]=pre,size[u]=1;
    for(int i=T.first[u];i;i=T.e[i].nxt){
        int v=T.e[i].v;
        if(v==pre) continue;
        dfs1(v,u);
        size[u]+=size[v];
        if(size[v]>size[son[u]]) son[u]=v;
    }
}
inline void dfs2(int u,int tp){
    top[u]=tp;
    if(son[u]){
        dfs2(son[u],top[u]);
    }
    for(int i=T.first[u];i;i=T.e[i].nxt){
        int v=T.e[i].v;
        if(v==fa[u]||v==son[u]) continue;
        dfs2(v,v);
    }
}
inline int LCA(int x,int y){
    while(top[x]!=top[y]){
        if(dep[top[x]]<dep[top[y]]) swap(x,y);
        x=fa[top[x]];
    }
    if(dep[x]<dep[y]) return x;
    return y;
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=m;i++){
        int x=read(),y=read();
        G.link(x,y);
    }
    tarjan(1);
    dfs1(1,0);
    dfs2(1,1);
    Q=read();
    while(Q--){
        int x=read(),y=read(),p=LCA(x,y);
        printf("%d\n",(dep[x]+dep[y]-2*dep[p])/2+1);
    }
}