数据降维-PCA主成分分析

1.什么是PCA？

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

数学原理：

目标函数：投影的维度上数据的方差最大

我们如何得到这些包含最大差异性的主成分方向呢？

事实上，通过计算数据矩阵的协方差矩阵，然后得到协方差矩阵的特征值特征向量，选择特征值最大(即方差最大)的k个特征所对应的特征向量组成的矩阵。这样就可以将数据矩阵转换到新的空间当中，实现数据特征的降维。

2.鸢尾花例子

 import numpy as np
 import matplotlib.pyplot as plt
 %matplotlib inline

 # decomposition降解
 # 化学变化降解之后得到的数据和原来的数据不一样，成分变了，属性变了
 # PCA将原来的属性变少，少量的数据可以代表原来比较多的数据
 from sklearn.decomposition import PCA
 from sklearn.linear_model import LogisticRegression
 from sklearn import datasets
 from sklearn.model_selection import train_test_split

 X,y=datasets.load_iris(True)
 # n_components 保留多少特征，取权重靠前的 whiten 标准化
 # 标准化：输出范围是负无穷到正无穷
 # 归一化：输出范围在0-1之间
 pca=PCA(n_components=0.95,whiten=False)
 X_pca=pca.fit_transform(X)
 X_pca[:10]

3.PCA的原理（可以去查看源码）

 # 1.去中心化，取平均值的意思
 B=X-X.mean(axis=0)

 # 2.计算协方差 协方差矩阵 bias表示偏差
 V=np.cov(B,rowvar=False,bias=True)

 # 3.计算协方差矩阵的特征值和特征向量 矩阵的概念
 # eig表示从大到小
 eigen,ev=np.linalg.eig(V)
 # 若挑选出百分之95的，找出权重在前95%，若不够，则加一，可多不可少
 cond=(eigen/eigen.sum()).cumsum()>=0.95
 index=cond.argmax()
 vector=ev[:,:index+1]

 # 4.降维标准，2个特征，选取两个最大的特征值所对应的的特征的特征向量
 # 百分比，计算各特征值所占的权重，累加
 vector=ev[:,:2]

 # 5.进行矩阵运算
 pca_result=B.dot(vector)
 pca_result[:10]

预测出来的结果：

特征值分解：

(1) 特征值与特征向量

如果一个向量v是矩阵A的特征向量，将一定可以表示成下面的形式：

其中，λ是特征向量v对应的特征值，一个矩阵的一组特征向量是一组正交向量。

实对称矩阵不同特征值的特征向量正交

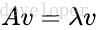
(2) 特征值分解矩阵

对于矩阵A，有一组特征向量v，将这组向量进行正交化单位化，就能得到一组正交单位向量。特征值分解，就是将矩阵A分解为如下式：

其中，Q是矩阵A的特征向量组成的矩阵，则是一个对角阵，对角线上的元素就是特征值。

这个其实就是根据 实对称矩阵不同特征值的特征向量正交这句话推导得来的，

这两个结论我推导了一下，请参考：

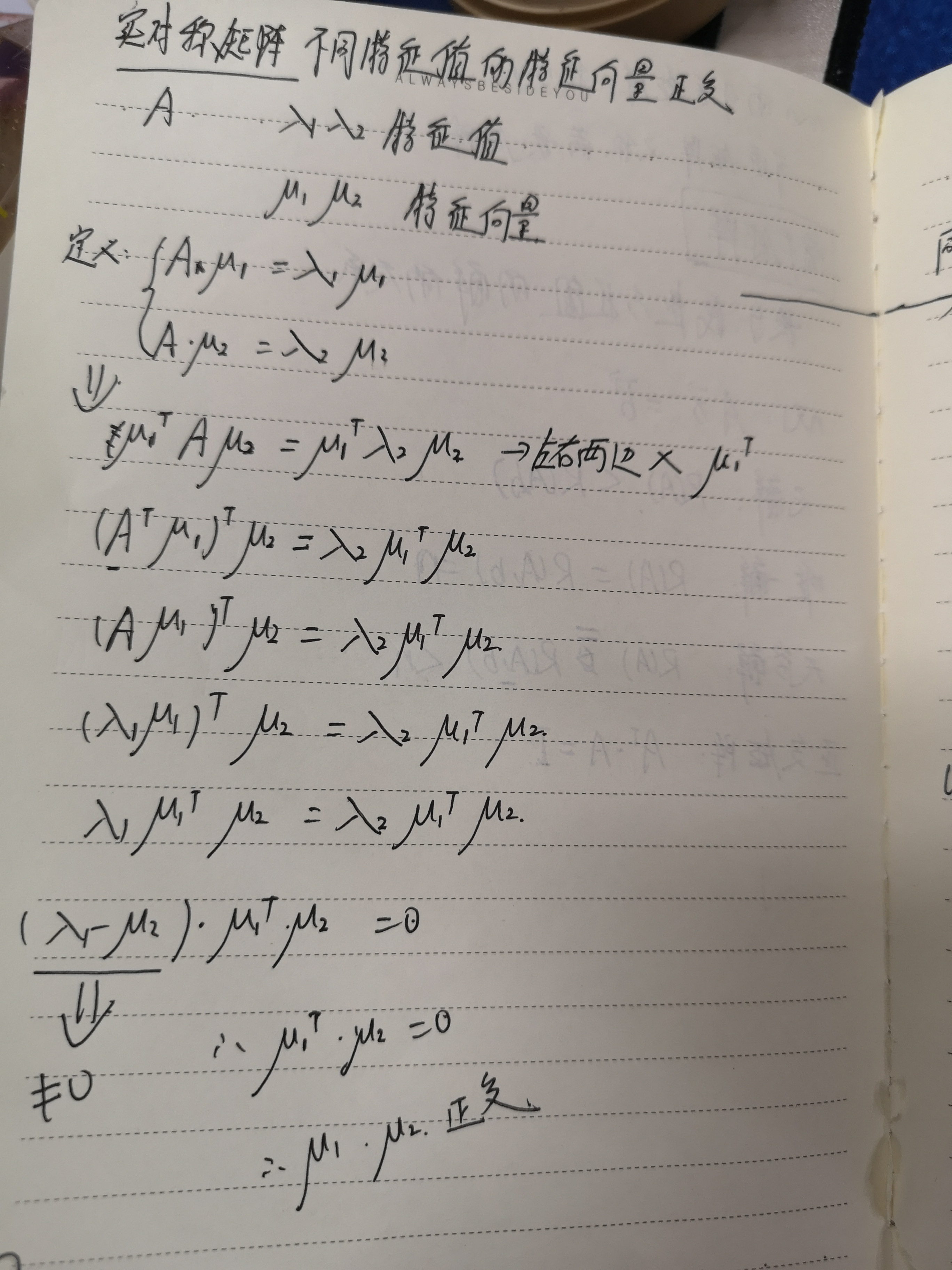
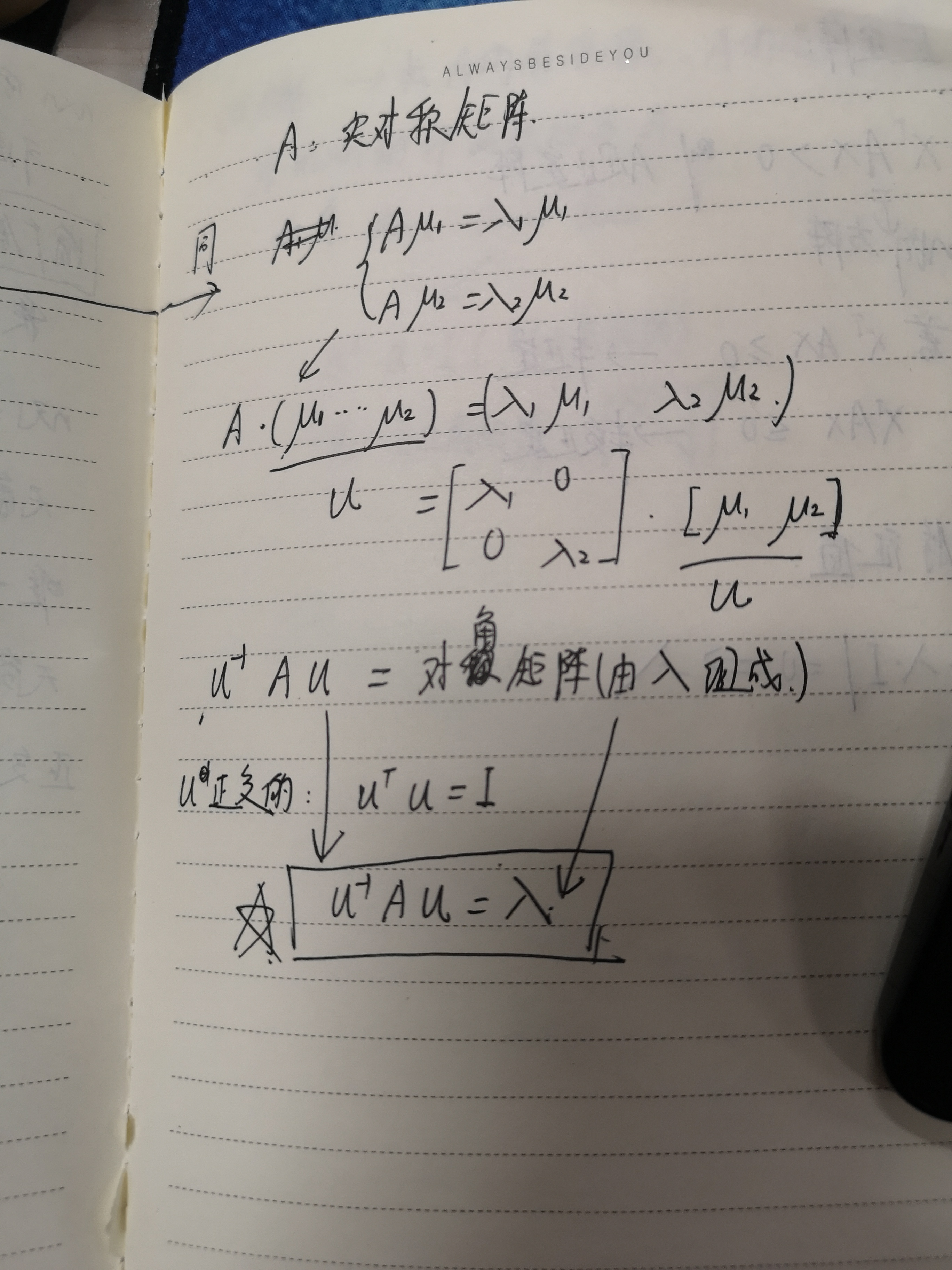
再举个例子：

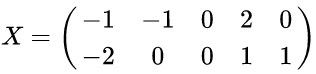
以X为例，我们用PCA方法将这两行数据降到一行。

1)因为X矩阵的每行已经是零均值，所以不需要去平均值。

2)求协方差矩阵：

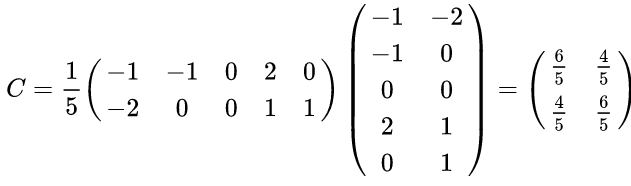
3)求协方差矩阵的特征值与特征向量。

求解后的特征值为：

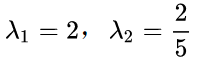
对应的特征向量

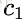
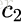
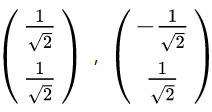
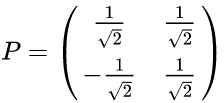
其中对应的特征向量分别是一个通解，和可以取任意实数。那么标准化后的特征向量为：

最后我们用P的第一行乘以数据矩阵X，就得到了降维后的表示：

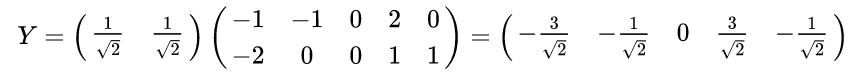
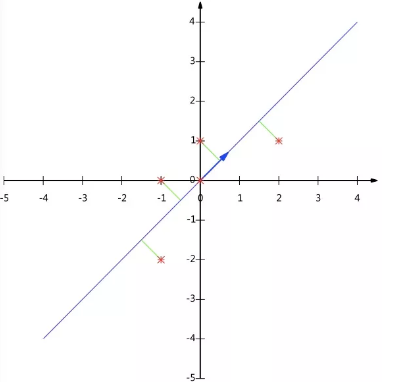
数据矩阵X降维投影结果：