【记录】OJ｜区间DP｜石子合并（环形）

1. 题干

描述

在一个园形操场的四周摆放N堆石子,现要将石子有次序地合并成一堆.规定每次只能选相邻的2堆合并成新的一堆，并将新的一堆的石子数，记为该次合并的得分。

试设计出一个算法,计算出将N堆石子合并成1堆最大得分.

输入

第1行一个正整数N,1≤N≤2000,表示有N堆石子.

第2行有N个数,分别表示每堆石子的个数.

输出

共1行,最大得分

输入样例1

4
4 4 5 9

输出样例1

54

2. 解

1) 原理概述

以最大值为例。

本问题采用了分冶的思想，是先求解小区间中的解，再合并到大区间中。

Fmax[i][j]意为区间[i,j]内合并的最大得分，t[i][j]意为区间[i,j]中的石子总分。

① 状态转移方程：

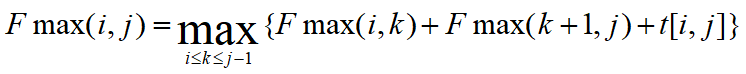
② 经过平行四边形优化后的状态转移方程：

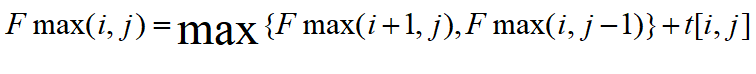
平行四边形优化的结论：使两堆的合并值最大的分割点，一定将堆[i,j]分成[i+1,j],[i,i]或者[i,j-1],[j,j]这两堆。
证明：(下图来自 HUST 课堂，笔者根据自己的理解将证明完善并添加了颜色和符号标记)

③ 环状结构优化(下图来自 HUST 课堂)：

2) 代码实现（以循环结构为例）：

#include<stdio.h>
#pragma warning(disable:4996)
#define TYPE_ull unsigned long long
//DP问题
TYPE_ull t[4005] = { 0 };
TYPE_ull F[4005][4005] = { 0 }, Max = 0;
TYPE_ull max(TYPE_ull i, TYPE_ull j)
{
	if (i > j)
		return i;
	else return j;
}
TYPE_ull f(int n)
{
	Max = 0;
	//F[i][j]意为区间(i,j)内合并的最大得分
	//for (int i = 1; i <= n; ++i)
	//{

	//	F[i][i + 1] = t[i + 1] - t[i - 1];//取相邻两数合并得分为两数之和
	//}
	//for (int i = 1; i <= n; ++i)
	//{
	//	F[i][i + 2] = max(F[i][i + 1], F[i + 1][i + 2]) + t[i + 2] - t[i - 1];//取间隔为2的F区间
	//}
	//...
	for (int v = 1; v < n; ++v)//间隔为v，从间隔为1算起，将递归转换为循环，算间隔为n-1为止即可
	{
		for (int i = 1; i <= 2 * n; ++i)
		{
			if (i + v < 2 * n)//注意不能越界
				F[i][i + v] = max(F[i][i + v - 1], F[i + 1][i + v]) + t[i + v] - t[i - 1];//取间隔为v的F区间
		}
	}
	for (int i = 1; i <= n; ++i)
	{
		Max = max(F[i][n + i - 1], Max);
	}
	return Max;
}

int main()
{
	int n, k;
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
	{
		scanf("%d", &k);
		t[i] = t[i - 1] + k;
	}
	for (int i = 1; i <= n; ++i)
	{
		t[n + i] = t[n] + t[i];
	}
	printf("%llu\n", f(n));
	return 0;
}

3) 笔者被坑到的地方

1. 迭代转循环：分冶思想，若直接计算F[1][n]这个最大问题，那么小问题还没算出来，最终的结果肯定是错的。为了计算小问题，可以将所有的小问题从最小的开始求。设定间隔为1，先写一个求解所有间隔为1的循环：

for (int i = 1; i <= n; ++i)
{
	F[i][i + 1] = t[i + 1] - t[i - 1];//取相邻两数合并得分为两数之和
}

然后再写间隔为2的：

for (int i = 1; i <= n; ++i)
{
	F[i][i + 2] = max(F[i][i + 1], F[i + 1][i + 2]) + t[i + 2] - t[i - 1];//取间隔为2的F区间
}

最后把间隔处理成一个新的循环即可。

1. 边界处理：要算间隔为1到(n-1)的所有区间，但是注意，当区间的初值为i的时候，它的末值最大仍然只能取n，区间长度最多为(n-i)。