DeepSeek又在节前放大招！

写在前面

事情是这样的，就在五一假期开始前夕，DeepSeek放出了模型DeepSeek-Prover-V2-671B：

这是延续了节假日狂飙的传统？

言归正传，我们看看这次放出了哪些核心技术。

最直接的方法是参见技术报告，也在半夜放出来了（真是一群勤奋的家伙啊）。

链接：https://github.com/deepseek-ai/DeepSeek-Prover-V2/blob/main/DeepSeek_Prover_V2.pdf，网络不方便的小伙伴可以关注公众号xiaoxi666后回复“DeepSeek_Prover_V2”获取。

这篇论文到底说了啥呢，先画个大纲总结下：

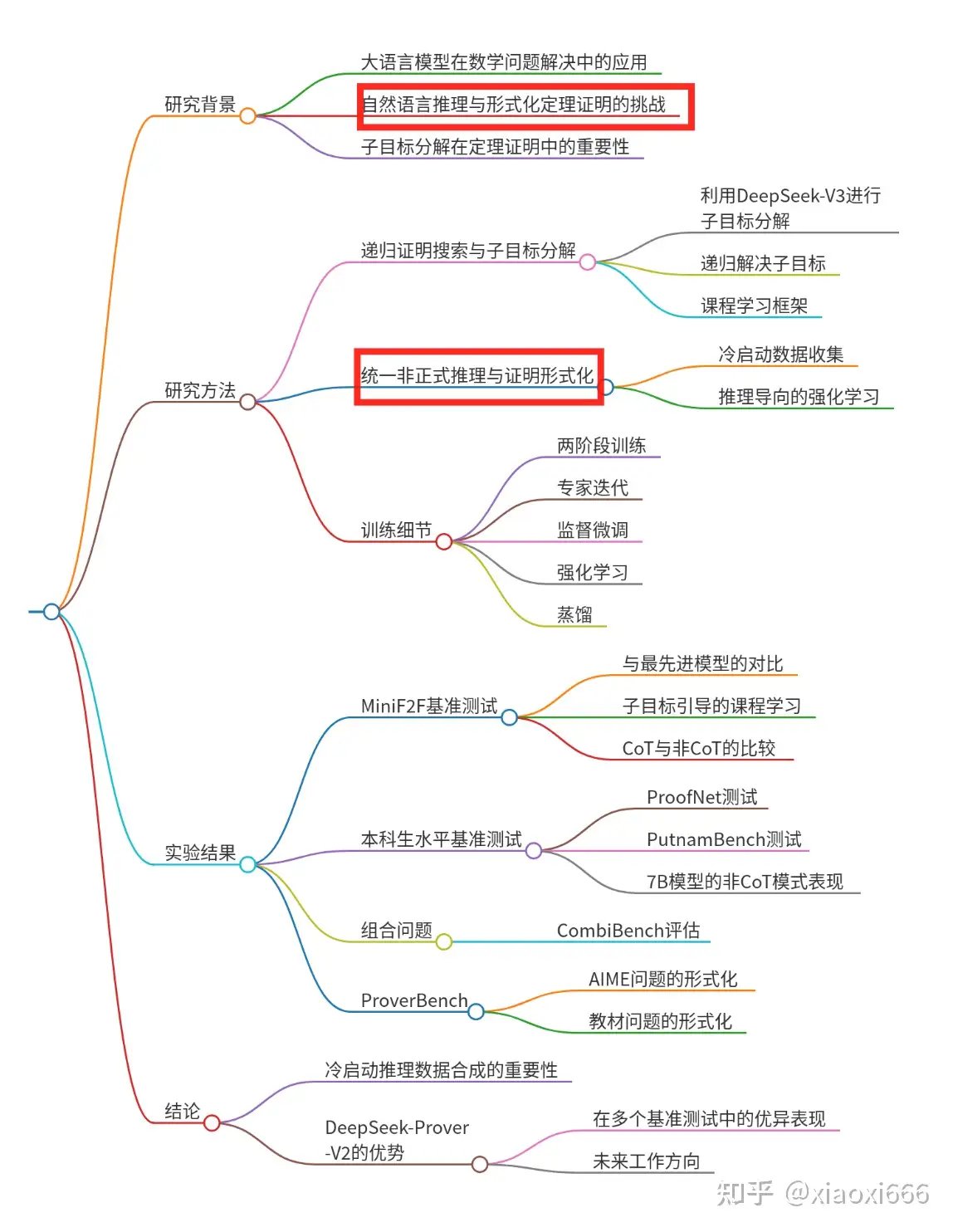
通篇读下来，印象最深刻的就是”形式化数学推理“和”形式化证明“这两个概念，他们两者的结合也是这个模型最大的创新点。

“非形式数学推理”与“形式化证明”

非形式数学推理的英文名为 informal mathematical reasoning，指使用自然语言和直观的逻辑来理解和解释数学概念或证明定理。它依赖于人类的直觉和经验，通常不涉及严格的符号和规则。

形式化证明的英文名为 formally verified 或者 formal theorem proving，指使用严格的数学符号和逻辑规则来构建和验证数学证明，要求每一步都必须有明确的依据，并且整个证明过程必须是可验证的。现在模型推理引入该方法，称为“形式化数学推理”，英文名为 formal mathematical reasoning。

两者的区别主要在于表达方式的精确性：

特点	非形式化推理	形式化推理
表达方式	自然语言	严格的数学符号和逻辑规则
精确性	较低，可能包含模糊表述	高，每一步都有明确依据
适用范围	日常交流、初步探索	严格证明、软件验证
工具和技术	直觉、经验、自然语言处理	形式化语言、自动定理证明器
示例	因为三角形内角和为180度，所以这个三角形是直角三角形。	根据欧几里得几何公理，若∠A + ∠B + ∠C = 180°，且∠A = 90°，则该三角形为直角三角形。

在深度学习和人工智能领域，非形式化推理和形式化证明的结合变得越来越重要（尤其数学定理证明时）：

非形式化推理可以帮助模型理解问题的背景和上下文，生成初步的证明思路。
形式化推理则用于将这些思路转化为严格的数学证明，确保每一步都是正确的。

通过结合这两种方法，可以更有效地解决复杂的数学问题，提高模型的推理能力和证明的准确性。这也是 DeepSeek-Prover-V2 主要发力点。

其实，早在2024年12月20日，就有一篇论文“Formal Mathematical Reasoning: A New Frontier in AI”讨论了形式化数学推理在人工智能领域中的重要性，这篇论文主要围绕4个点进行了研究：

1、形式化数学推理的定义：形式化数学推理基于形式系统，如一阶逻辑、依赖类型理论和带有形式规范的计算机程序。这些系统提供了一个环境，可以验证模型的推理并提供自动反馈。

2、证明工具的使用：同样是引入了Lean这种用于编写形式证明的函数式编程语言。它适用于编写数学定义、定理和证明，其核心特性是能够自动检查证明的 correctness。

3、自动形式化：自动形式化是将非正式数学文本自动转换为形式数学表达式的过程。这可以通过机器学习和深度学习技术实现，如神经机器翻译和自回归语言模型。

4、神经定理证明：神经定理证明是利用深度学习方法在形式系统中寻找定理证明的启发式方法。常用的方法包括专家迭代、从错误中学习和非正式证明草图的利用。

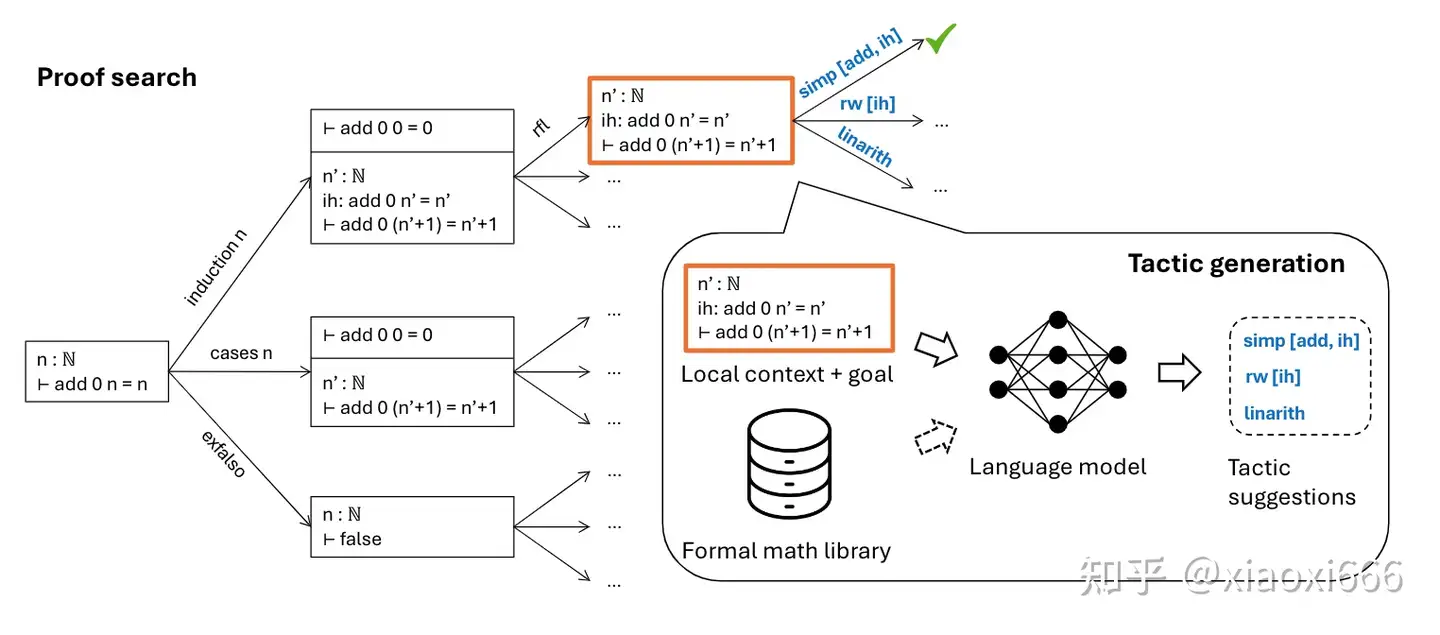
其实，在AIGC时代以前，形式化验证的手段常用于安全关键的系统（例如航空航天、高铁动车、核电等），其系统的行为必须是可以预测的，形式化方法能够确保这些系统的行为符合预期，避免死锁、数据竞争等问题。更为具体的描述可参见往期文章：

有没有一种测试技术，能够确保软件不存在Bug？：mp.weixin.qq.com/s/xCgmoOlH27Ft4Z8q5rGagw

可以预见的是，未来的强人工智能，会朝着越来越严谨的推理方向演进（虽然AGENT、RAG等外挂技术还是当下主流）。引入形式化验证的方法，对于迈向强人工智能之路具有极为重要的意义。

Lean4 与 ADT

提到 Lean4，就不得不提一下 ADT，它们有很深的渊源。ADT的全称是 Algebraic Data Types，一般译为“代数数据类型”。ADT 是 Lean4 的核心组成部分，用于定义数据结构、逻辑命题和数学对象，并通过模式匹配和递归机制支持函数定义和证明。

比如，在Lean4中，可以使用inductive关键字来定义 ADT。例如，定义布尔类型 Bool 和自然数类型 Nat：

inductive Bool where

  | false : Bool

  | true : Bool

inductive Nat where

  | zero : Nat

  | succ (x : Nat) : Nat

上述定义分别创建了布尔类型和自然数类型，其中布尔类型有两个构造函数 false 和 true，自然数类型有两个构造函数 zero 和 succ。

更为复杂的数学结构和数据模型也可以定义，比如定义一个简单的二叉树结构：

inductive Tree (α : Type) where

  | leaf : Tree α

  | node : Tree α → α → Tree α → Tree α

上述定义创建了一个参数化的二叉树类型，其中 leaf 表示空树，node 表示一个包含左子树、值和右子树的节点。

模式匹配功能也不在话下，比如定义一个函数来计算二叉树的大小：

def treeSize {α : Type} : Tree α → Nat

  | leaf => 0

  | node left _ right => 1 + treeSize left + treeSize right

总的来说，Lean4 通过支持 ADT 提供了强大的数据定义和操作能力，这使得它在形式化数学和自动化定理证明中非常有用。另外，Lean4 的强大类型系统和元编程能力进一步巩固了它在这些领域的应用潜力。

最后，可以参考往期文章，其中有一篇推荐文章，结合ADT和代数解空间进行了详细阐述：