【填算符】（log 值域的做法）

比赛在这里呢

填算符

下发题解说的神马东西，赛时根本想不到

讲一个赛时想得到的 \(O(n\log 值域)\) 的思路，很好理解

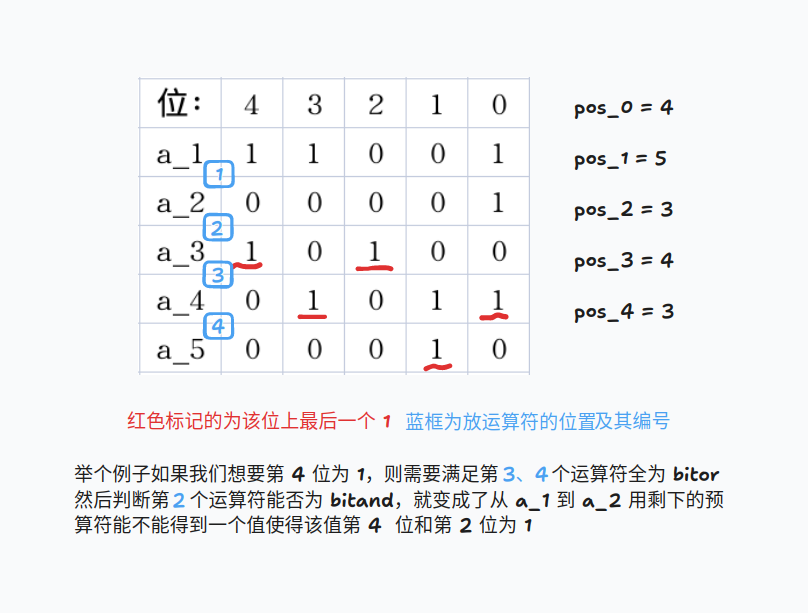
我们处理出二进制下每一位上的 1 的最后一次出现的位置，将第 \(i\ (i\in[0,60])\) 位上的 1 最后一次出现的位置记作 \(pos_i\)

同时我们设 \(H=n-k-1\) 为总共有的 bitor 的操作数

有以下结论：由于 \(pos_i\) 是 \(i\) 位上最后一个 1，所以一旦它后面放了一个 与，这一位上就是 0 了；若我们想要这一位为 1，必须至少满足从 \(pos_i\) 到最后的运算符全是 bitor。

发现有以下情况：

• 若 \(n-pos_i>H\)，即 \(pos_i\) 之后需要放的运算符的数量比 bitor 的总操作数多，也就是说在 \(pos_i\) 之后我一定需要放 bitand 操作，所以这种情况下这一位一定不对答案有贡献

• 若 \(n-pos_i<H\)，也就是说我可以从 \(pos_i\) 的前一个位置开始到最后全放 bitor 操作，那么这样第 \(i\) 位上可以是 1，为了使值最大，所以第 \(i\) 位上一定要是 1，所以从第 \(pos_i\) 位到最后必须全是 bitor 操作，对于这种情况的 \(i\) 我们记为合法位

• 若 \(n-pos_i=H\)，也就是说从第 \(pos_i\) 到最后的运算符可以全是 bitor 操作，但 \(pos_i\) 的前一位只能是 bitand
  
  所以我们特判从第 1 个位置到 \(pos_i\) 的前一位全放 bitand 能不能让到第 \(pos_i\) 个数时得到的值第 $\forall $ \(j 满足 [pos_j=pos_i]\) 位为 1，若能则该位也为合法位，否则不合法

对于所有合法位的 \(pos\) 取最小值设为 \(end\)，因为已经保证 \(end\) 到最后的预算符全是 bitor，此时有一下两种可能，而我们想尽量构成第二种可能：

1. \(end\) 的前一位预算符也为 bitor，这样我们一定能达到答案最大了，想使答案最优直接让从 \(end-2\) 开始的 \(k\) 个运算符为 bitor 就好了

2. \(end\) 的前一位在某些情况为 bitand 也是可以使答案最大的，所以我们判断能不能让 \(end\) 的前一位为 bitand 同样使答案最大；
   
   发现可以的条件相当于从第 \(end-1\) 个数到最前面用仅剩的 bitor 操作得到一个答案，使得这个答案第 $\forall $ \(i 满足 [pos_i=end]\) 位为 1，若能满足条件则第 \(end-1\) 个操作符为 bitand。

满足条件的判断又和上述的第三个情况判断一致了，相当于以 \(end-1\) 为下界，再做一次求 \(min(合法的\ pos)\)，实质上是不断的递归。

所以一个递归 \(dfs(end, H)\) 表示下界为 \(end\)，还剩 \(H\) 个 bitor 操作，判断能不能得到我想要的答案：

若不能则直接从第 \(end-2\) 开始的 \(k-res\) 个运算符全为 bitand 就是答案（\(res\) 为在之前的递归中已经确定的 bitand 的个数）

若能则第 \(end-1\) 个位置可以为 bitand，并设 \(end'=min(这一层中合法的\ pos)\)，继续递归 \(dfs(end',H-(end-end'))\) 判断第 \(end'-1\) 个位置能不能为 bitand。

形式化如下：