SciTech-Mathmatics-Analysis: important inequalities 重要的几个不等式: Trigonometry + Mean + Cauchy + Minkowski + Newton + Bernoulli + Chebyshev + Hölder

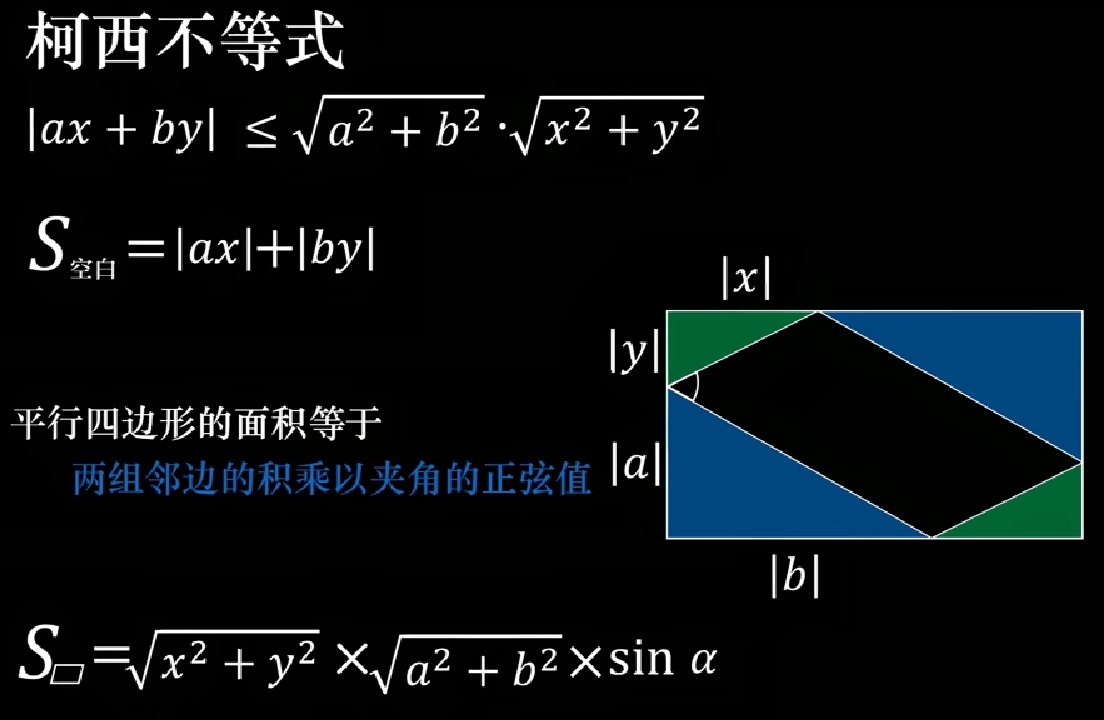
• Cauchy Inequality(柯西不等式):

---

\(\large \begin{array}{rl} \\
| ax +by | &<= & \sqrt{a^2+b^2} \cdot \sqrt{x^2+y^2} \\
& \because & | ax +by | \leq |ax| + |by| = \sqrt{a^2+b^2} \cdot \sqrt{x^2+y^2} \cdot \sin{\alpha} \\
\end{array}\)

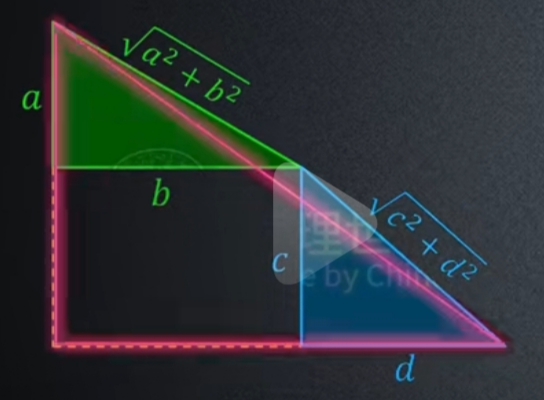
• Minkowski inequality

---

$\large \sqrt{a^2 + b^2} + \sqrt{c^2 + d^2} \geq \sqrt{(a+c)^2+(b +d)^2} $

• 权方和 inequality

---

1. 均值不等式

---

\(\large Q_n = \dfrac{ a_1 + a_2 + \cdots + a_n } {n}, \text{ 算数平均数 }\)

\(\large Q_n = \sqrt{ \dfrac{ a_1^2 + a_2^2 + \cdots + a_n^2 } {n} }, \text{ 平方平均数 }\)

1. 排序不等式

---

1. Trigonometry inequality

---

1. Newton inequality

---

1. Bernoulli inequality

---

1. Chebyshev inequality
   
   

2. Hölder Inequality