奇怪吸引子---Russler
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性、稳定性、吸引性。吸引子是一个数学概念,描写运动的收敛类型。它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出发的非定常流的所有轨道都趋于它,这样的集合有很复杂的几何结构。由于奇怪吸引子与混沌现象密不可分,深入了解吸引子集合的性质,可以揭示出混沌的规律。
这里会展示利用奇怪吸引子生成的艺术图像。奇怪吸引子通常含有三维或四维的数据,而图像是二维的,因此可以从不同的位面将奇怪吸引子投影到二维图像中。
原图及数学公式取自:
http://chaoticatmospheres.com/125670/1204030/gallery/strange-attractors

这里使用自己定义语法的脚本代码生成混沌图像,相关软件参见:YChaos生成混沌图像。如果你对数学生成图形图像感兴趣,欢迎加入QQ交流群: 367752815。
脚本代码:
[ScriptLines]
u=-(j + k)
v=i+a*j
w=b+k*(i - c)
i=i+u*t
j=j+v*t
k=k+w*t
x=i
y=j [Variables]
a=0.200000
b=0.200000
c=5.700000
i=1.000000
j=1.000000
k=1.000000
t=0.001000
混沌图像:


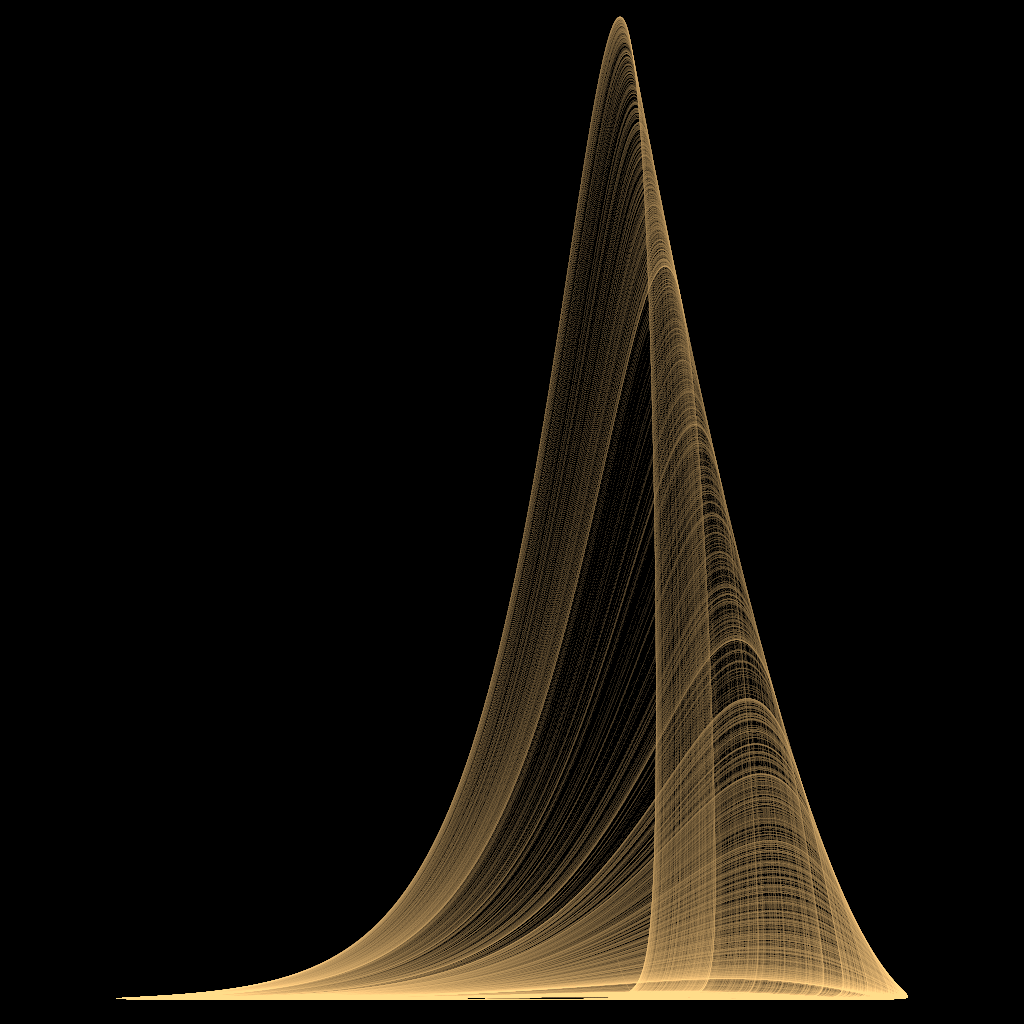
奇怪吸引子---Russler的更多相关文章
- 奇怪吸引子---YuWang
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WimolBanlue
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---WangSun
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---TreeScrollUnifiedChaoticSystem
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Thomas
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---ShimizuMorioka
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Sakarya
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---Rucklidge
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
- 奇怪吸引子---RayleighBenard
奇怪吸引子是混沌学的重要组成理论,用于演化过程的终极状态,具有如下特征:终极性.稳定性.吸引性.吸引子是一个数学概念,描写运动的收敛类型.它是指这样的一个集合,当时间趋于无穷大时,在任何一个有界集上出 ...
随机推荐
- Pair Project: Elevator Scheduler [电梯调度算法的实现和测试]
作业提交时间:10月9日上课前. Design and implement an Elevator Scheduler to aim for both correctness and performa ...
- Vrapper-Eclipse的vim插件安装方法
Vrapper是一款Eclipse的插件,使在Eclipse下编辑文档时可以像使用Vim一样. 它有两种安装方法,在线安装和安装包安装: 在线安装: 打开Eclipse,Help->Instal ...
- netbeans中实体类代码的bug
用了netbeans中实体类代码后,忽然报错: com.sun.tools.javac.code.Symbol$CompletionFailure: 找不到sun.util.logging.Platf ...
- Win2012R2的一个Bug---安装群集后可能引发的软件崩溃问题及相应补丁
如标题,笔者查阅资料发现微软声称安装故障转角色后就可能发生上述描述问题,但不止于SSMS崩溃.建议使用win2012R2的朋友安装补丁. 笔者在部署win2012R2+Sql2014 cluster时 ...
- jquery 插件原则
区分开 Dom 对象,jQuery Dom对象, Json数据. Dom对象是诸如: document.getElementById 返回的原生Dom对象. jQuery Dom对象,如:$(&quo ...
- 实验七 状态机设计ADC0809采样控制电路
一.实验目的 学习用状态机实现A/D转换器ADC0809的采样控制电路. 二.实验内容 利用QuartusⅡ实现A/D转换器ADC0809的采样控制电路状态机设计:给出仿真波形.最后进行引脚锁定并进行 ...
- 04-Vue入门系列之Vue事件处理
4.1. 监听事件的Vue处理 Vue提供了协助我们为标签绑定时间的方法,当然我们可以直接用dom原生的方式去绑定事件.Vue提供的指令进行绑定也是非常方便,而且能让ViewModel更简洁,逻辑更彻 ...
- 【软件架构】IM架构设计(安卓版)
1. 架构总览 2. 模块介绍 2.1 协议封装与任务流程 2.1.1 协议与任务的封装 协议有协议头(协议头因为格式相同,被抽象出来)和协议体组成,协议有两类:请求协议(request)和回复协议( ...
- [读书笔记]C#学习笔记七: C#4.0中微小改动-可选参数,泛型的可变性
前言 下面就开始总结C#4.0的一些变化了, 也是这本书中最后的一点内容了, 这一部分终于要更新完了. 同时感觉再来读第二遍也有不一样的收获. 今天很嗨的是武汉下雪了,明天周六,一切都是这么美好.哈哈 ...
- Atitit.词法分析的原理 理论
Atitit.词法分析的原理 理论 1. 分词 .词法分析lexical analysis 1 1.1. 分词主要流程 1 1.2. 分词的属性如下表token 1 1.3. 词法分析器主要包括:构造 ...
