2016"百度之星"-资格赛

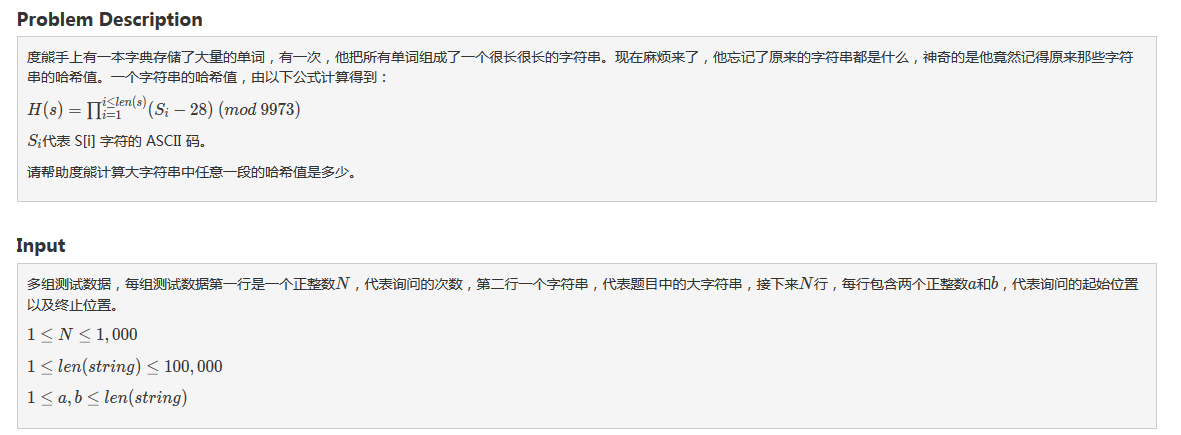
本题要求:(Ar*A2...An)%p,亦即[(A1*A2*...An)/(A1*A2*...Ar-1)]%p,由于A1*A2...An乘积过大,无法求得相除所得的结果

我们需要用到乘法逆元(a*k≡1 (mod p)的k值就是a关于p的乘法逆元),而乘法逆元有如下定理®:(a*k) mod p结果与(a/b) mod p等价,其中k为b关于p的乘法逆元

而由费马小定理(已知p是质数且gcd(a, p) = 1，则 a^p-1 ≡ 1 (mod p),  所以 a*a^p-2 ≡ 1 (mod p))知,a^(p-2)就是a的逆元了求解,利用快速幂运算计算(补充:亦可用扩展欧几里得求解)

注意具体求a时，应不断对p取mod

#include <stdio.h>
#include <string.h>
#define LEN 100001
#define P 9973

/*注意:转化为s时,必须从1开始,因为如果a=1,那么在做快速幂时,会用到s[-1],造成下标越界*/
void Transform(char *s1,int *s){
	int i;
	s[0]=1;
	for(i=1;i<=strlen(s1);i++) //the entire len
		s[i]=s[i-1]*(s1[i-1]-28)%P;
}

void HashValue(int a,int b,int *s){
	//s[b]*s[a-1]^(p-2) mod p
	//quickmod
	int res,tmp,n;
	n = P-2;
	res = 1;
	tmp = s[a-1];//s必须从1开始取
	while(n){
		if(n&1)
			res=(res*tmp)%P;
		n >>=1;
		tmp=(tmp*tmp)%P;
	}

	printf("%d\n",s[b]*res%P);
} 

int main(){
	int n,a,b,i,s[LEN];
	char s1[LEN];
	while(scanf("%d",&n)!=EOF){
		getchar();
		gets(s1);
		Transform(s1,s);
		for(i=0;i<n;i++){
			scanf("%d%d",&a,&b);
			HashValue(a,b,s);
		}
	}
	return 0;
}

定理 ®的证明:

由:b*k≡1 (mod p)有b*k=p*x+1，k=(p*x+1)/b
将k代入(a*k) mod p，得：
[a*(p*x+1)/b]mod p
=[(a*p*x)/b+a/b]mod p(注意:只要a整除b,自然有(a*p*x)整除b)
={[(a*p*x)/b] mod p +(a/b)} mod p
={[p*(a*x)/b]mod p +(a/b)} mod p,而p*[(a*x)/b] mod p=0

=(a/b) mod p

参考资料:

　　[1]http://blog.csdn.net/nickwong_/article/details/38797629

[2]http://www.cnblogs.com/tiankonguse/archive/2012/08/14/2638949.html

[3]http://blog.csdn.net/jklongint/article/details/51415402

Time:20:48:52 2017-03-01