最速下降方法和Newton方法

最速下降方法
- Euclid范数和二次范数
  - Euclid范数
  - 二次范数
    - 基于坐标变换的解释
- 采用$\ell_1$-范数的最速下降方向
  - 数值试验
Newton 方法

《Convex Optimization》

最速下降方法

$f(x+v)$在$v=0$处的一阶泰勒展开为：

\[f(x+v)\approx \hat{f}(x+v) = f(x) + \nabla f(x)^{T}v
\]

$\nabla f(x)^{T}v$是$f$在$x$处沿$v$的方向导数。它近似给出了$f$沿小的步径$v$会发生的变化。

在$v$的大小固定的前提下，讨论如何选择$v$使得方向导数最小是有意义的，即：

\[\Delta x_{nsd}= argmin\{\nabla f(x)^{T}v \:|\: \|v\|=1\}
\]

最速下降方向就是一个使$f$的线性近似下降最多的具有单位范数的步径。注意，这里的单位范数，并不局限于Euclid范数。

我们先给出最速下降方法的算法，再介绍几种范数约束。

Euclid范数和二次范数

Euclid范数

显然，这时的方向就是负梯度方向。

二次范数

我们考虑二次范数

\[\|z\|_P=(z^TPz)^{1/2}=\|P^{1/2}z\|
\]

其中P为n阶对称正定矩阵。

这时的最优解为：

\[\Delta x_{nsd}=-(\nabla f(x)^{T}P^{-1}\nabla f(x))^{-1/2}P^{-1}\nabla f(x)
\]

这个最优解，可以通过引入拉格朗日乘子，求解对偶函数KKT条件获得，并不难，就不写了。

基于坐标变换的解释

二次范数，可以从坐标变换的角度给出一个解释。

我们定义线性变换：

\[\bar{u}=P^{1/2}u
\]

那么：

\[g(\bar{u})=f(P^{-1/2}\bar{u})=f(u)
\]

$g$在$\bar{x}$出的负梯度方向为：

\[\Delta \bar{x}=-\nabla \bar{f}(\bar{x})=-P^{-1/2}\nabla f(P^{-1/2}\bar{x})=-P^{-1/2}\nabla f(x)
\]

注意，并没有归一化。

又，我们已经知道$\Delta x = -P^{-1} \nabla f(x)$(只是方向而已)，所以：

\[\Delta \bar{x}=P^{1/2}\Delta x
\]

同样的线性变换。换言之，二次范数$\|\cdot\|_P$下的最速下降方向可以理解为对原问题进行坐标变换$\bar{x}=P^{1/2}x$后的梯度方向。辅以下图便于理解。

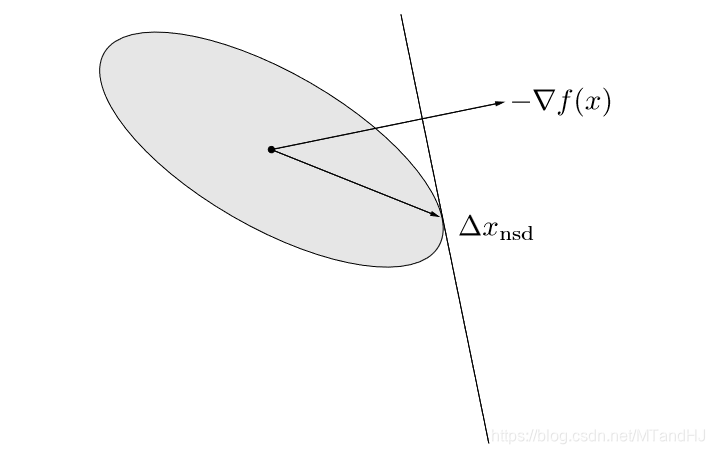
采用$\ell_1$-范数的最速下降方向

这个问题的刻画如下：

\[\Delta x_{nsd}=argmin\{\nabla f(x)^Tv \: | \: \|v\|_1=1\}
\]

$\ell_1$即各分量绝对值之和，所以，只需把$\nabla f(x)$绝对值分量最大的那个部分找出来即可。不妨设，第$i$个分量就是我们要找的，那么：

\[\Delta x_{nsd}=-sign(\frac{\partial f(x)}{\partial x_i})e_i
\]

其中，$e_i$表示第$i$个基向量。

所以，在每次下降过程中，都只是改变一个分量，所以$\ell_1$-范数的下降，也称为坐标下降算法。

辅以下图以便理解：

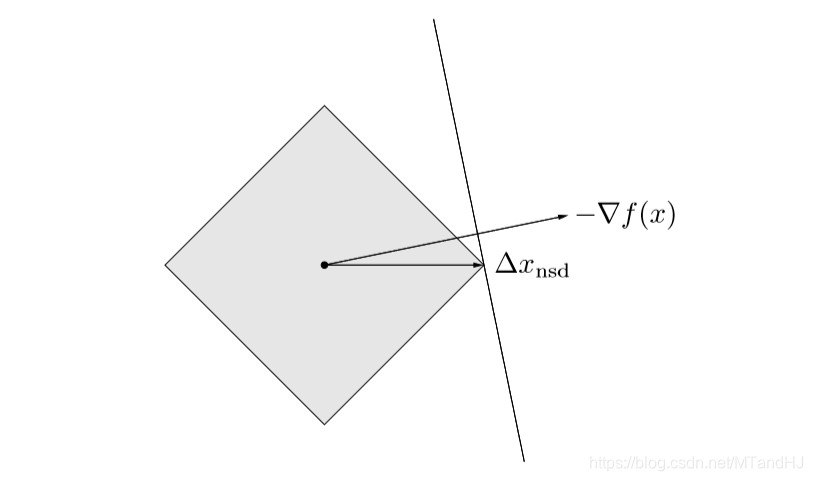
至于收敛性分析，与先前的相反，我们不在这里给出（打起来太麻烦了实际上，有需求直接翻书就好了）。

数值试验

我们依然选择$f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}$，$\alpha=0.2,\beta=0.7$，初始点为$(7, 3)$，下图为我们展示了一种较为极端的坐标下降的方式。

代码只需要改变gradient2的几行而已。

def gradient2(x):

    x0 = x[0]

    x1 = x[1]

    grad1 = np.exp(x0+3*x1-0.1) \

            + np.exp(x0-3*x1-0.3) \

            - np.exp(-x0-0.1)

    grad2 = 3 * np.exp(x0+3*x1-0.1) \

            -3 * np.exp(x0-3*x1-0.3)

    if abs(grad1) > abs(grad2):

        return np.array([grad1/abs(grad1),0])

    else:

        return np.array([0, grad2/abs(grad2)])

Newton 方法

最开始看的时候，还很疑惑，后来才发现，原来这个方法在很多地方都出现过。除了《凸优化》(《Convex Optimization》)，数学分析（华师大）和托马斯微积分都讲到过。虽然，或者将的一元的特殊情况，而且，后者的问题是寻找函数的零值点。起初，还不知道怎么把俩者联系起来，仔细一想，导函数的零值点不就是我们所要的吗？当然，得要求函数是凸的。

实际上，Newton方法是一种特殊的二次范数方法。特殊在，$P$的选取为Hessian矩阵$\nabla^2 f(x)。$我们还没有分析，二次范数的$P$应该如何选择。在下降方法的收敛性分析中，我们强调了条件数的重要性。加上刚刚分析过的坐标变换，坐标变换后，新的Hessian矩阵变为：

\[P^{-1/2}\nabla^2 f(x)P^{-1/2}
\]

所以，如果我们取$P =\nabla^2f(x^*)$，那么新的Hessian矩阵在最有点附近就近似为$I$，这样就能保证快速收敛。如果，每次都能选择$P=\nabla^2 f(x)$，这就是Newton方法了。下图反映了为什么这么选择会加速收敛：

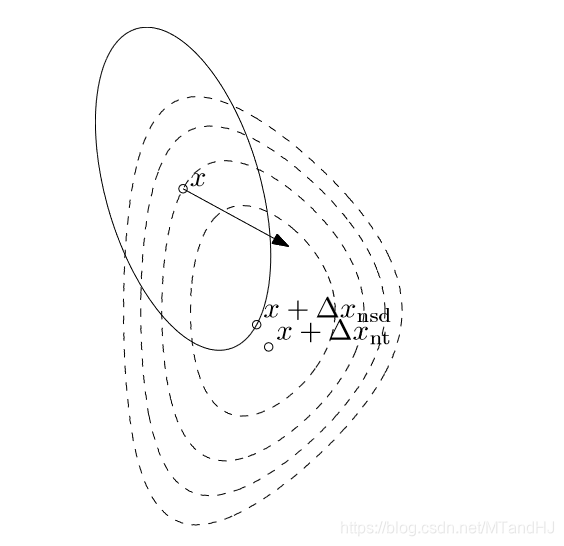
Newton 步径

Newton步径：

\[\Delta x_{nt}=-\nabla^2 f(x)^{-1}\nabla f(x)
\]

则：

\[\nabla f(x)^T\Delta x_{nt}=-\nabla f(x)^T\nabla^2f(x)^{-1}\nabla f(x)<0
\]

因为我们假设Hessian矩阵正定，所以上述不等式在$\nabla f(x) \ne 0$时都成立。

二阶近似的最优解

$f(x+v)$在$v=0$处的二阶近似为：

\[\hat{f}(x+v)=f(x)+\nabla f(x)^Tv+\frac{1}{2}v^T \nabla^2f(x)v
\]

这是$v$的二次凸函数，在$v=\Delta x_{nt}$处到达最小值。下图即是该性质的一种形象地刻画：

线性化最优性条件的解

如果我们在$x$附近对最优性条件$\nabla f(x^*)=0$处进行线性化，可以得到：

\[\nabla f(x+v) \approx \nabla f(x) + \nabla^2 f(x) v=0
\]

这个实际上就是我在最开始对Newton方法的一个解释。不多赘述。

Newton 步径的仿射不变性

这个在代数里面是不是叫做同构？

Newton 减量

我们将

\[\lambda (x)=(\nabla f(x)^T \nabla^2 f(x)^{-1}\nabla f(x))^{1/2}
\]

称为Newton减量。

有如下的性质：

\[f(x) = \mathop{inf} \limits_{y} \hat{f}(y)=f(x)-\hat{f}(x+\Delta x_{nt})=\frac{1}{2}\lambda (x)^2
\]

\[\lambda (x) = (\Delta x_{nt}^T \nabla^2f(x) \Delta x_{nt})^{1/2}
\]

\[\nabla f(x)^T \Delta x_{nt}=-\lambda (x)^2
\]

Newton步径同样是仿射不变的。

Newton步径常常用作停止准则的设计。

Newton 方法

算法如下：

收敛性分析

收敛性分为俩个阶段，证明比较多，这里只给出结果。

第一阶段为阻尼Newton阶段，第二阶段为二次收敛阶段。

数值实验

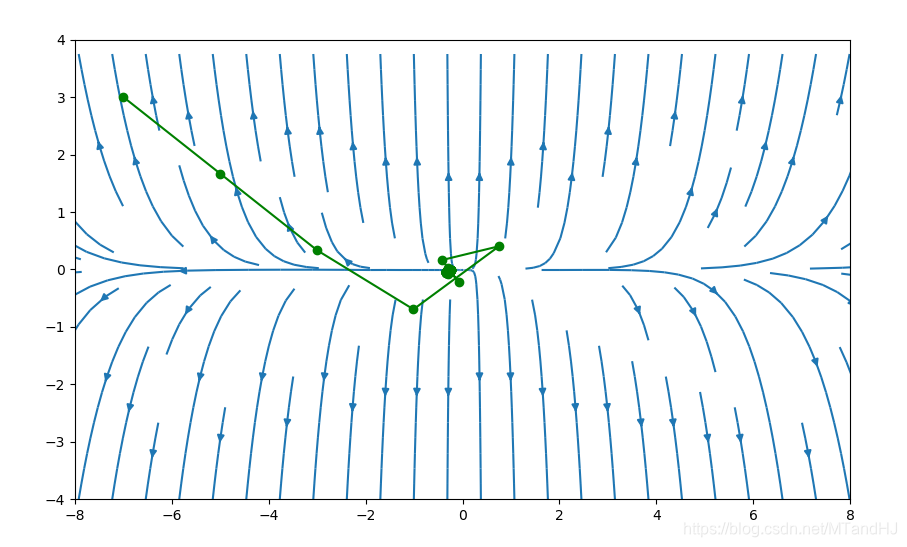
我们依然选择$f(x)=e^{x_1+3x_2-0.1}+e^{x_1-3x_2-0.1}+e^{-x_1-0.1}$，$\alpha=0.2,\beta=0.7$，初始点为$(7, 3)$，下图采用牛顿方法的图（代码应该没写错吧）。

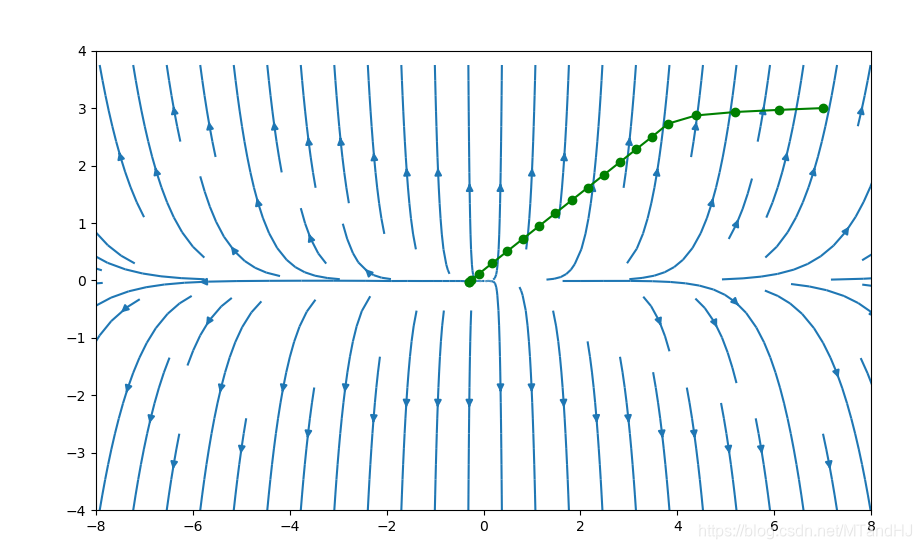
下图初始点为$(-5, 3)$

代码

def hessian(x):

    x0 = x[0]

    x1 = x[1]

    hessian = np.zeros((2, 2), dtype=float)

    element1 = np.exp(x0 + 3 * x1 - 0.1)

    element2 = np.exp(x0 - 3 * x1 - 0.1)

    element3 = np.exp(-x0 - 0.1)

    hessian[0, 0] = element1 + element2 + element3

    hessian[0, 1] = 3 * element1 - 3 * element2

    hessian[1, 0] = 3 * element1 - 3 * element2

    hessian[1, 1] = 9 * element1 + 9 * element2

    return np.linalg.inv(hessian)

下降方法也修改了一下：

    def grad3(self, gradient, alpha, beta, error=1e-5):

        """回溯直线收缩算法 Newton步径

        gradient: 梯度需要给出

        alpha: 下降的期望值 (0, 0.5)

        beta:每次更新的倍率 (0, 1)

        error: 梯度的误差限，默认为1e-5

        """

        assert hasattr(gradient, "__call__"), \

            "Invalid gradient"

        assert 0 < alpha < 0.5, \

            "alpha should between (0, 0.5), but receive {0}".format(alpha)

        assert 0 < beta < 1, \

            "beta should between (0, 1), but receive {0}".format(beta)

        error = error if error > 0 else 1e-5

        def search_t(alpha, beta, grad, hessian_inv):

        	"""回溯"""

            t = 2

            t_old = 2

            step = grad @ hessian_inv

            grad_module = grad @ step

            assert grad_module >= 0, "wrong in grad_module"

            while True:

                newx = self.x + t * step

                newy = self.__f(newx)

                if newy < self.y - alpha * t * grad_module:

                    return t_old

                else:

                    t_old = t

                    t = t_old * beta

        while True:

            grad = -gradient(self.x)

            hessian_inv = hessian(self.x)

            t = search_t(alpha, beta, grad, hessian_inv)

            x = self.x + t * grad @ hessian_inv

            lam = grad @ hessian_inv @ grad

            if lam / 2 < error: #判别准则变了

                break

            else:

                self.x = x

                self.y = self.__f(self.x)

                self.__process.append((self.x, self.y))