Pytorch中的自动求导函数backward()所需参数含义

摘要：一个神经网络有N个样本，经过这个网络把N个样本分为M类，那么此时backward参数的维度应该是【N X M】

正常来说backward（）函数是要传入参数的，一直没弄明白backward需要传入的参数具体含义，但是没关系，生命在与折腾，咱们来折腾一下，嘿嘿。

---

首先，如果out.backward()中的out是一个标量的话（相当于一个神经网络有一个样本，这个样本有两个属性，神经网络有一个输出）那么此时我的backward函数是不需要输入任何参数的。

运行结果：

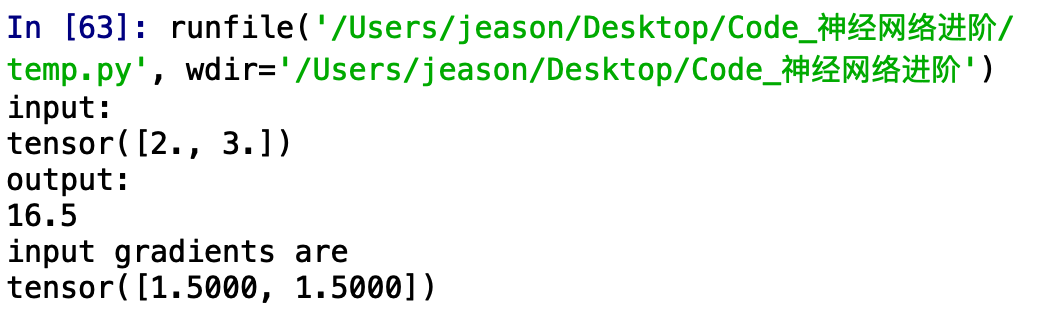
不难看出，我们构建了这样的一个函数：

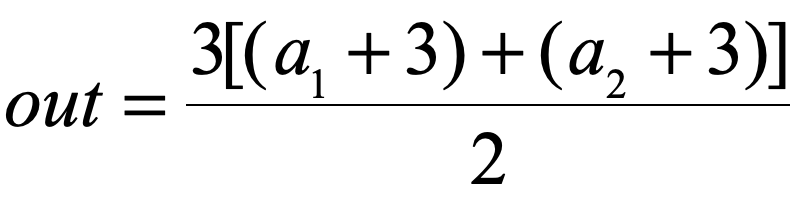
所以其求导也很容易看出：

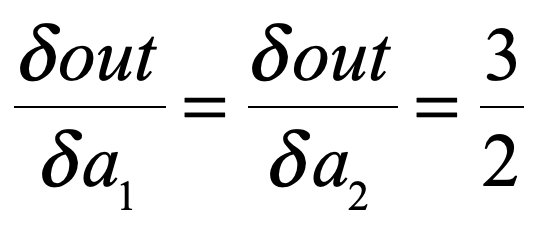
这是对其进行标量自动求导的结果

---

如果out.backward()中的out是一个向量（或者理解成1xN的矩阵）的话，我们对向量进行自动求导，看看会发生什么？

先构建这样的一个模型（相当于一个神经网络有一个样本，这个样本有两个属性，神经网络有两个输出）：

模型也很简单，不难看出out求导出来的雅克比应该是：

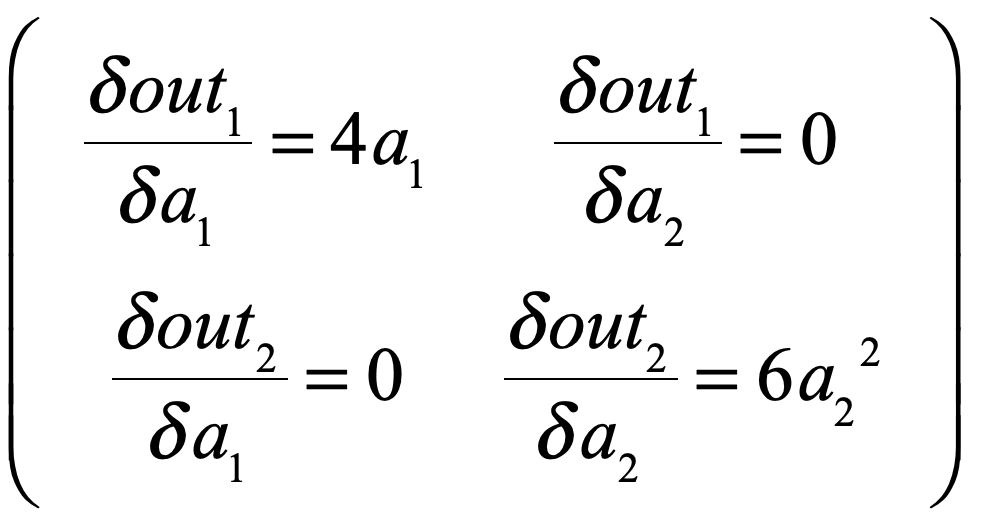，因为a1 = 2，a2 = 4，所以上面的矩阵应该是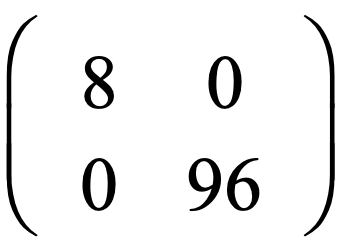  

运行的结果：

嗯，的确是8和96，但是仔细想一想，和咱们想要的雅克比矩阵的形式也不一样啊。难道是backward自动把0给省略了？

咱们继续试试，这次在上一个模型的基础上进行小修改，如下：

可以看出这个模型的雅克比应该是：

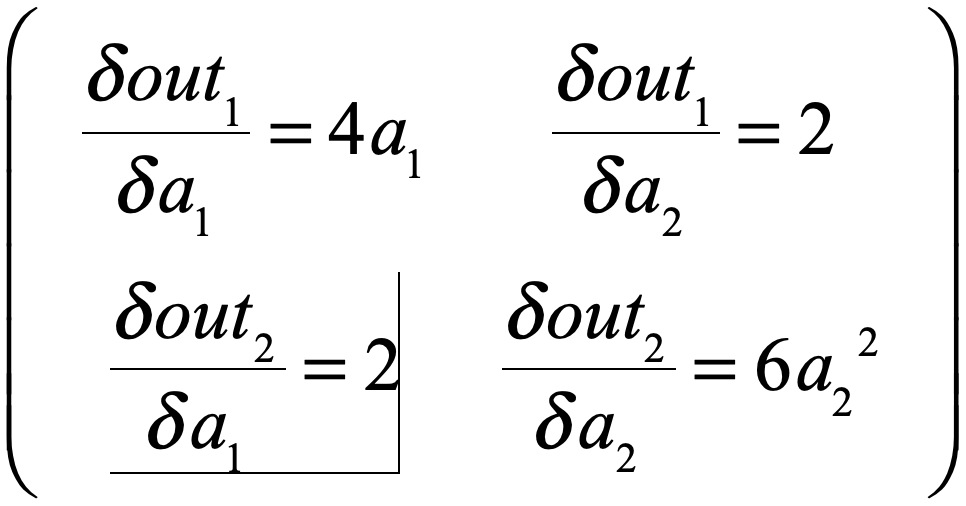
运行一下，看是不是：

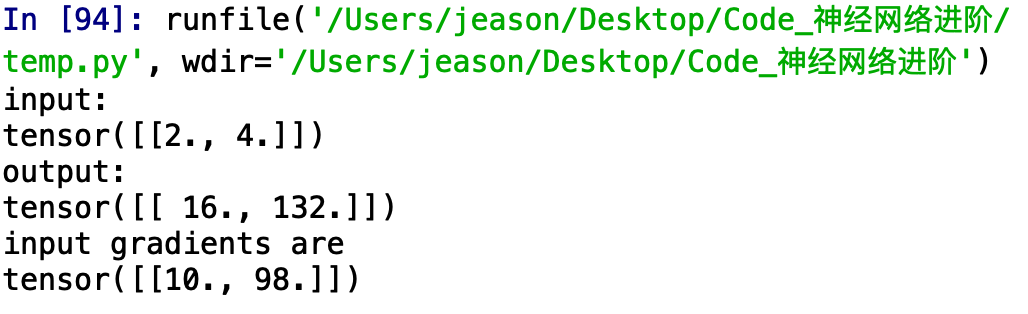
等等，什么鬼？正常来说不应该是  [ [ 8 , 2 ] , [ 2 , 96 ] ]么？

我是谁？我再哪？

为什么就给我2个数，而且是  8 + 2 = 10 ，96 + 2 = 98 。难道都是加的 2 ？

想一想，刚才咱们backward中传的参数是 [ [ 1 , 1 ] ]，难道安装这个关系对应求和了？

咱们换个参数来试一试，程序中只更改传入的参数为[ [ 1 , 2 ] ]：

运行一下：

嗯，这回可以理解了，我们传入的参数，是对原来模型正常求导出来的雅克比矩阵进行线性操作，可以把我们传进的参数（设为arg）看成一个列向量，那么我们得到的结果就是(注意这里是矩阵乘法，为了好表示我用了*):

( Jacobi * arg )^T

在这个题里，我们得到的实际是：

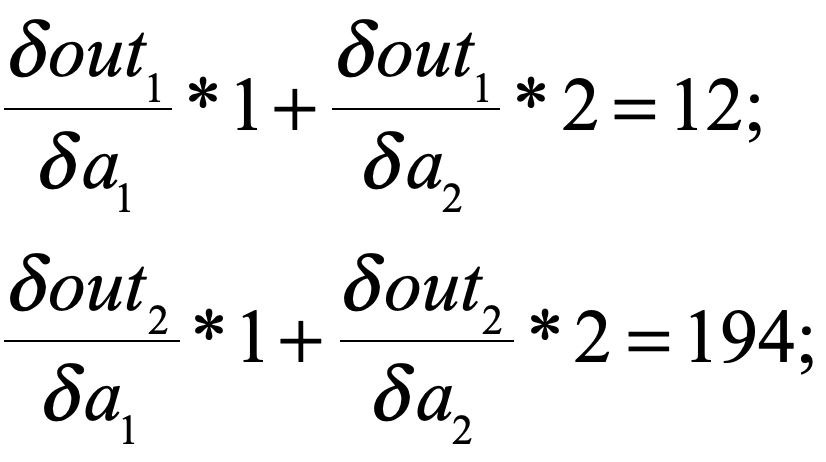
看起来一切完美的解释了，但是就在我刚刚打字的一刻，我意识到官方文档中说k.backward()传入的参数应该和k具有相同的维度，所以如果按上述去解释是解释不通的。

哪里出问题了呢？

仔细看了一下，原来是这样的：在对雅克比矩阵进行线性操作的时候，应该把我们传进的参数（设为arg）看成一个行向量（不是列向量），那么我们得到的结果就是(注意这里是矩阵乘法，为了好表示我用了*):

  ( arg * Jacobi )^T

即

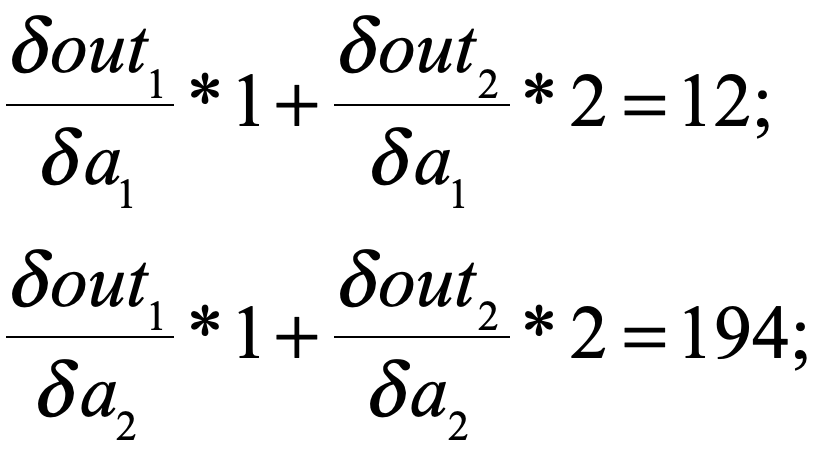
这回我们就解释的通了。

现在我们来输出一下雅克比矩阵吧，为了不引起歧义，我们让雅克比矩阵的每个数值都不一样（一开始分析错了就是因为雅克比矩阵中有相同的数据），所以模型小改动如下：

如果没问题的话咱们的雅克比矩阵应该是 [ [ 8 , 2 ] , [ 4 , 96 ] ]

好了，下面是见证奇迹的时刻了,不要眨眼睛奥，千万不要眨眼睛......

3

2

1

砰............

好了，现在总结一下：因为经过了复杂的神经网络之后，out中每个数值都是由很多输入样本的属性（也就是输入数据）线性或者非线性组合而成的，那么out中的每个数值和输入数据的每个数值都有关联，也就是说【out】中的每个数都可以对【a】中每个数求导，那么我们backward（）的参数[k₁,k₂,k₃....k_n]的含义就是：

　　　

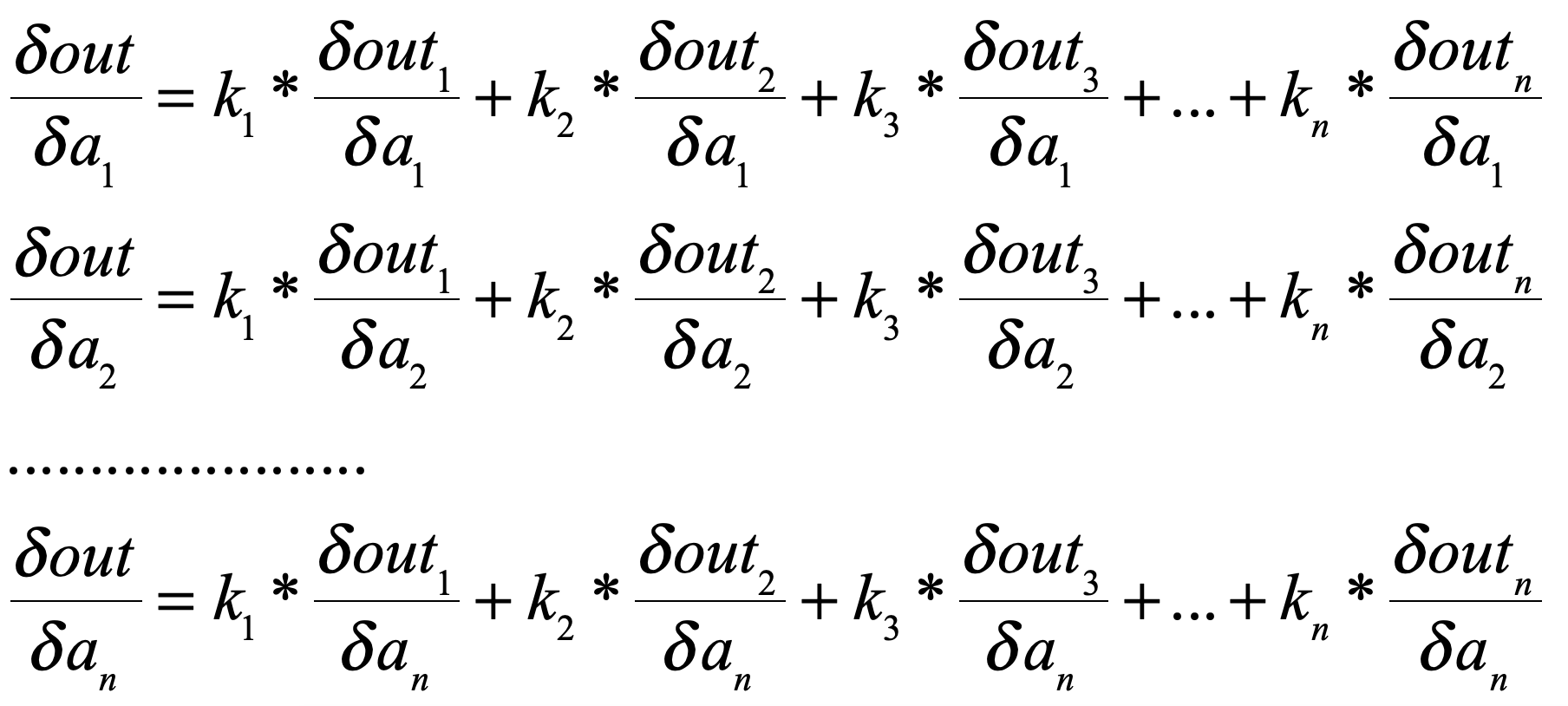
也可以理解成每个out分量对a_n求导时的权重。

---

现在，如果out是一个矩阵呢？

下面的例子也可以理解为：相当于一个神经网络有两个样本，每个样本有两个属性，神经网络有两个输出.

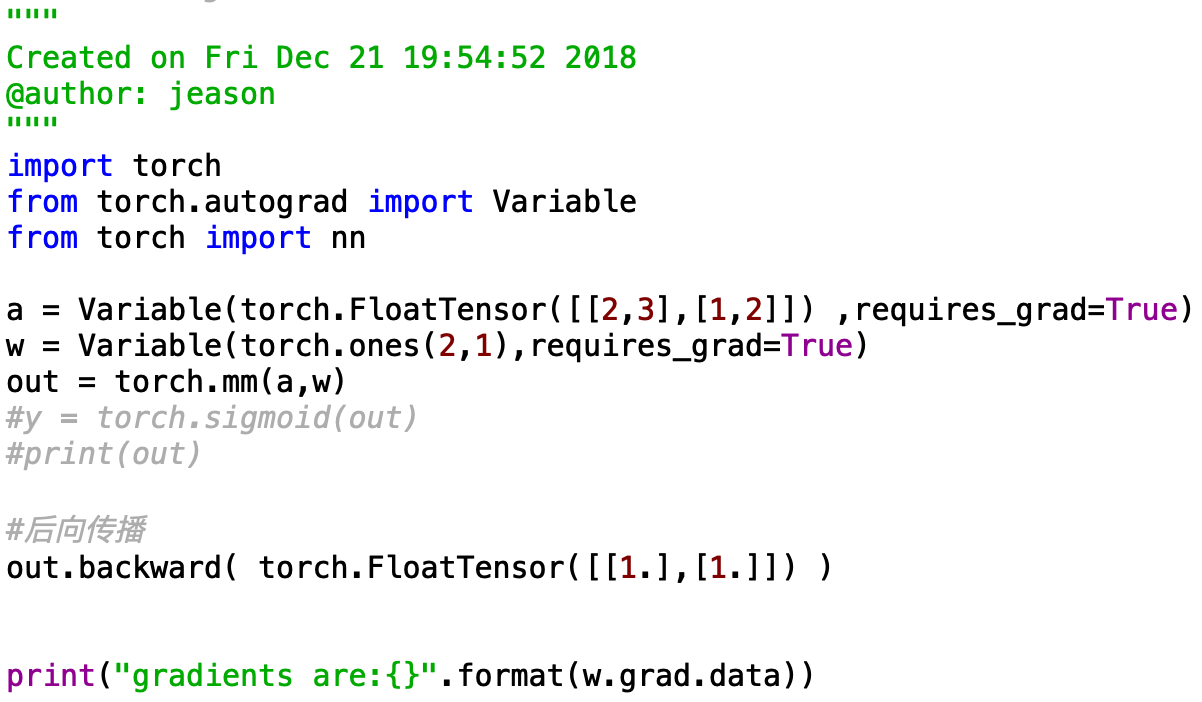
如果前面的例子理解了，那么这个也很好理解，backward输入的参数k是一个2x1的矩阵，2代表的就是样本数量，就是在前面的基础上，再对每个样本进行加权求和。

结果是：

如果有兴趣，也可以拓展一下多个样本的多分类问题，猜一下k的维度应该是【输入样本的个数 X 分类的个数】

好啦，纠结我好久的pytorch自动求导原理算是彻底搞懂啦~~~