Day 3 下午

依旧是组合数问题

• 先来看一道题

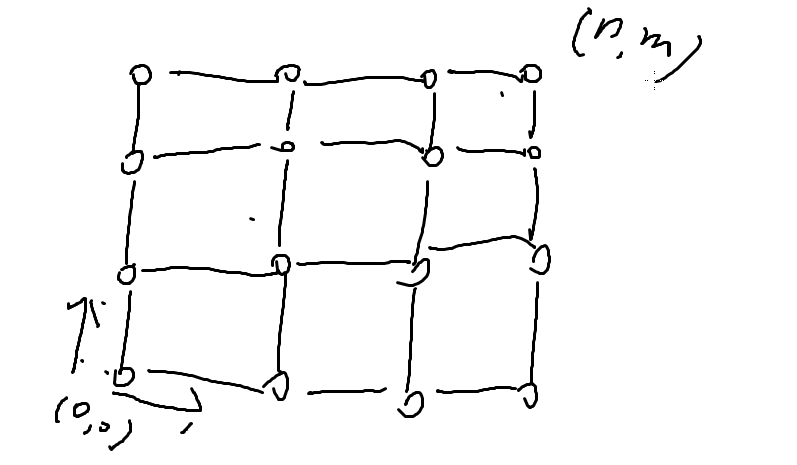
如图，一个n*m的方格中，从原点开始，每次只能向上走或者向右走，求走到点(n,m)共有多少种走法

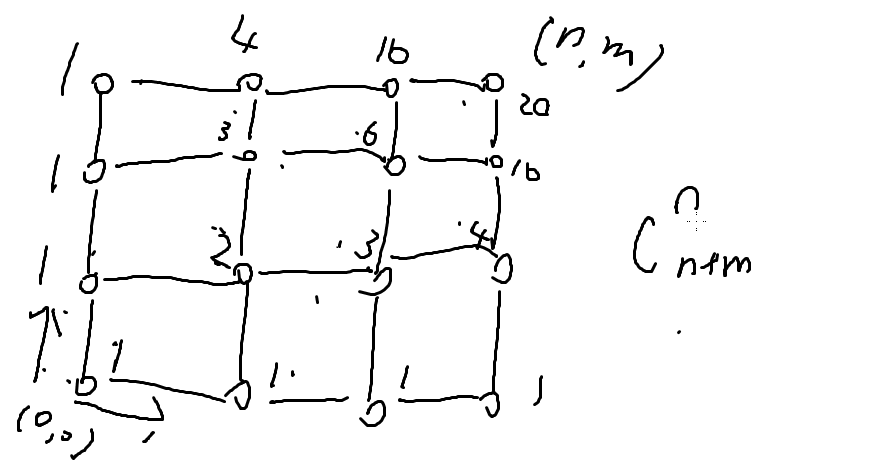
一般做法：

一个一个写，每一个节点的种数=它左边的数量+右边的数量

显然可以DP做

但我们不用DP做(滑稽

组合数：  ans=C(n+m,n)

原因：一共要走n+m步，从中选出n步向右走的，即为答案（C(n+m,m)也是一样滴）

• 经典题：问从(0,0)走到(n,m)且不穿过直线y=x的方案数，如图

总的方案减去不合法的方案

对称过去

一定经过(1,0)

 

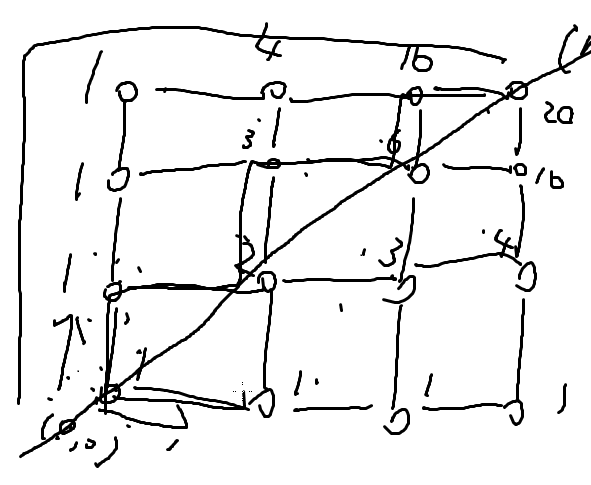
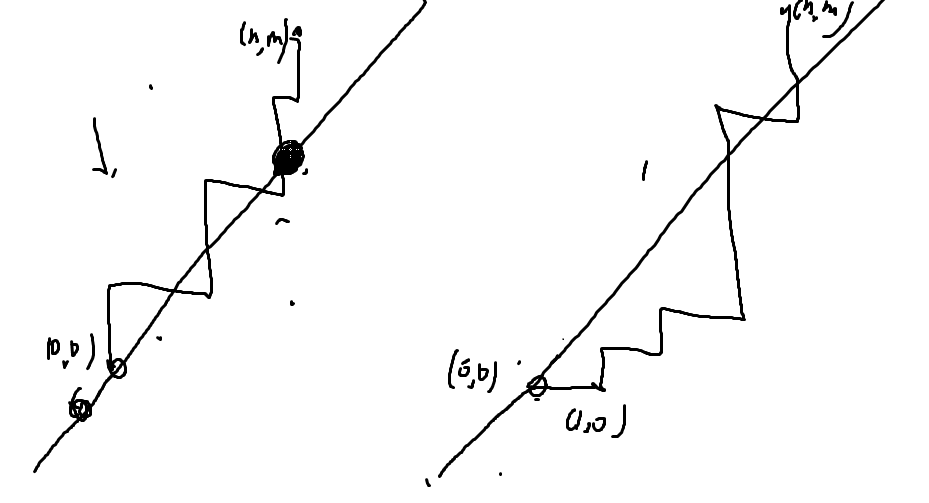
洛谷P4369

好吧其实这个题简单的一批.....

话说每一个1都可以写成C(n,0)d的形式.....

这下知道怎么做了吧

•1+1+1+1+...+1+(x-k+1)

•C(1  ,0)+c(2,0)+...

 

 

 

直接比较组合数是n！的复杂度，显然会tle，而且也不好算，我们可以转而比较log的大小

、

•求n!前缀和

•比较log

 

•两边展开，系数杨辉三角

 

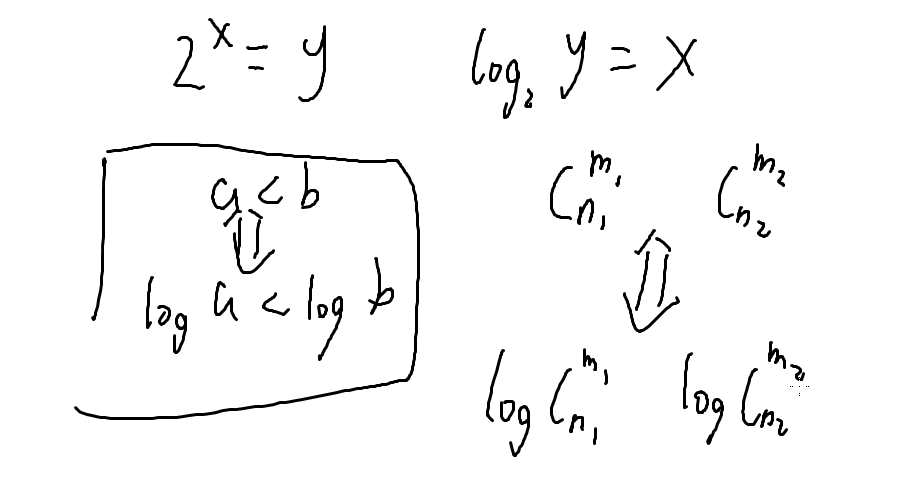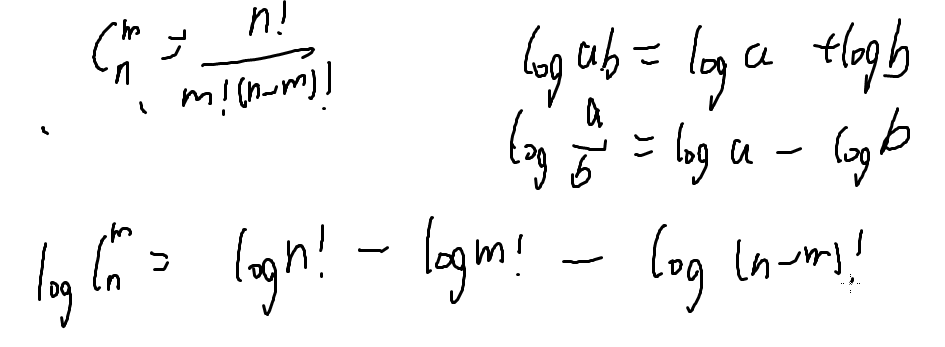
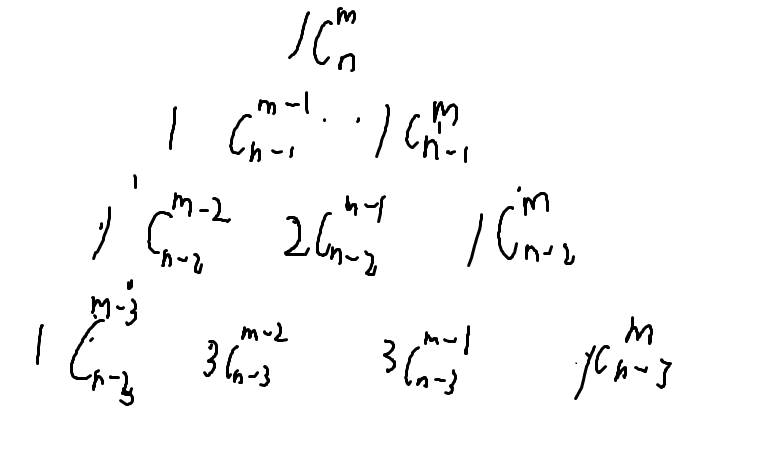
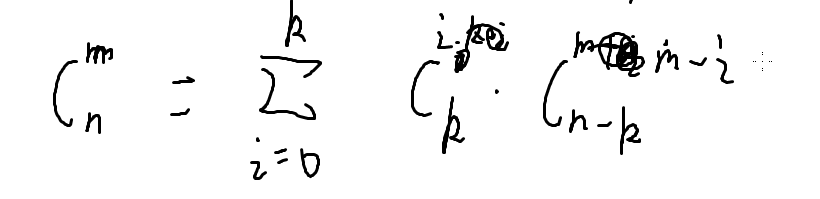
一个神奇的结论：

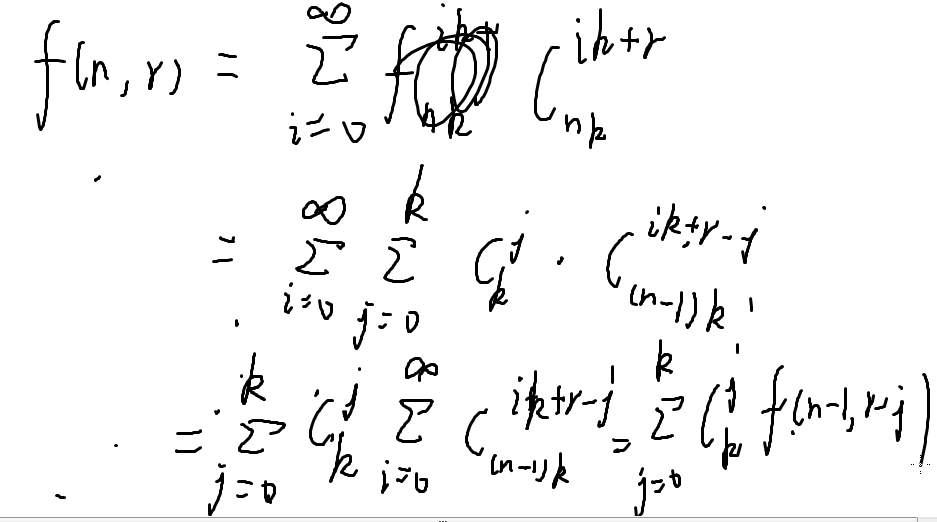
结合转移矩阵

放一篇自己写的题解（用杨辉三角做的）

然后我们来看另一种解法

Lucas定理

P为素数，则有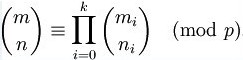

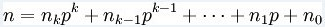
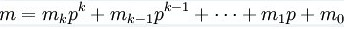
就是这样：

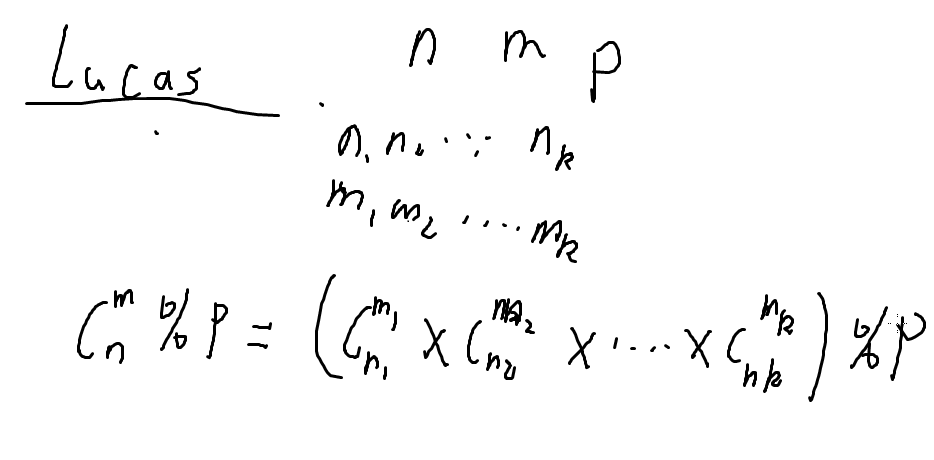
注：这里是将n，m转化为p进制

再来看这道题：

•因为C(n,m)是p的倍数，而C(ni,mi)中并不含有p，所以某一位有ni<mi使得它=0(这里原题是i，j，由于下标重复就用n和m了)

 容斥原理

已知∩的大小，求∪的大小

 

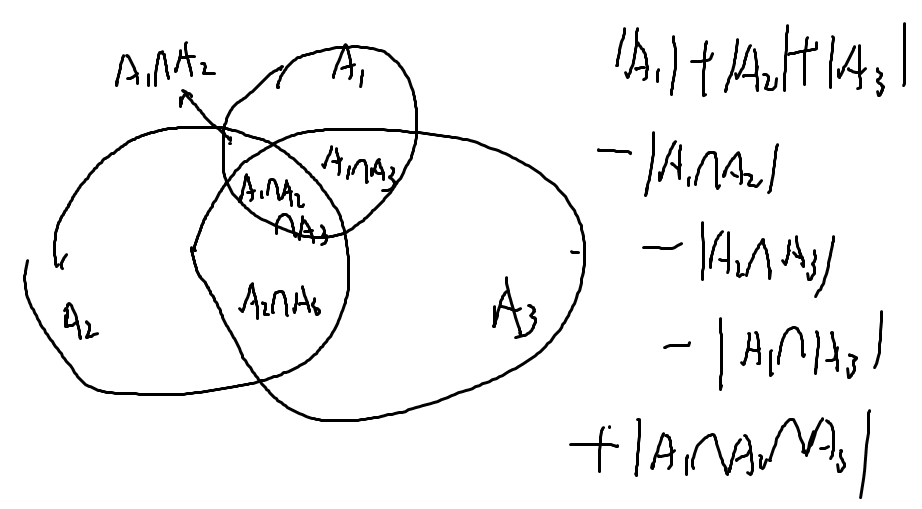
就是这样的

•170+130+120-45-20-22+3

 维恩图

•μ：数论函数的容斥系数

 

总的方案数减去有一个人不符合的方案数加上有两个人不符合的方案数以此类推

 

不考虑其他，n个人围成圈坐有(n-1)!种方案

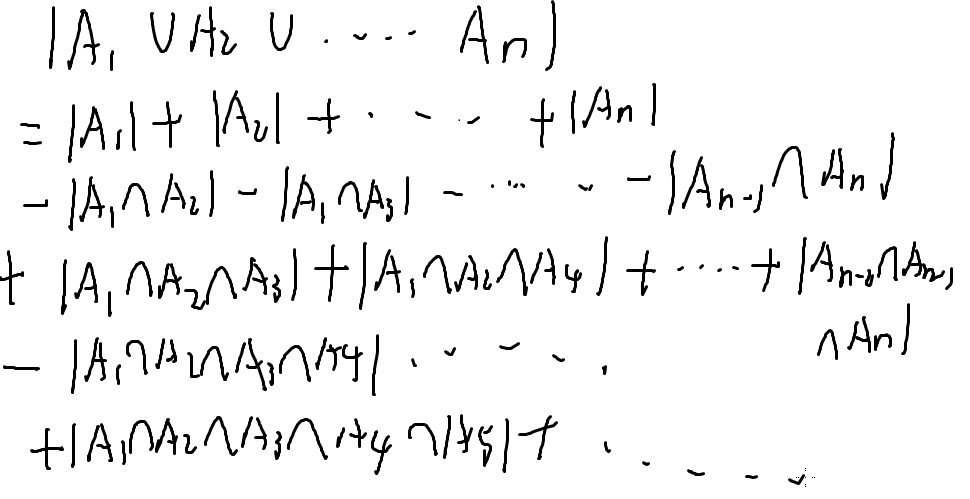
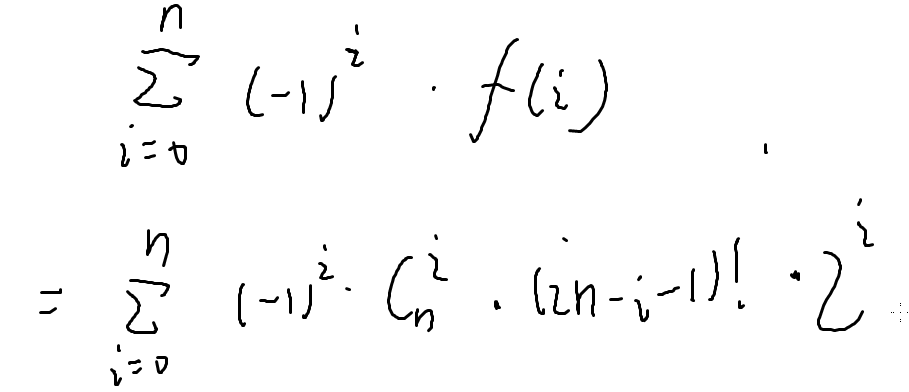
总结来了！

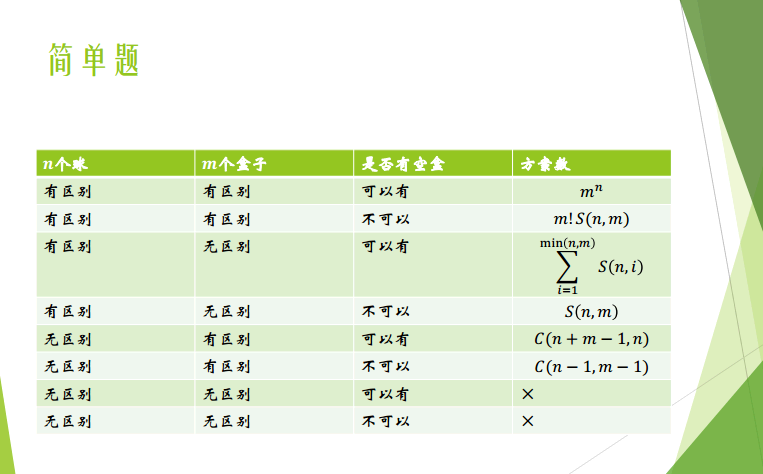
也是容斥原理

•不能打羽毛球的情况有：

•球  >=0      >=1      =0       

•拍   =0       =1        > =1 

   

结合起来就好了