MATLAB模拟布丰投针实验

MATLAB模拟布丰投针实验

标签（空格分隔）： 算法

---

Buffon's Needle

桌面上有距离为a的若干平行线，将长度为L的针随机丢在桌面上，则这根针与平行线相交的概率是多少？假定L < a.

思路：从针据横线的距离与夹角得出。

解决：

1. 假设针的中点到最近横线的距离为y，则\(y\in[0,\frac{a}{2}]\);

• 因为投针是随机的，所以y服从均匀分布：

\[ f(y) =
\begin{cases}
\frac{2}{a}, & \text{$0 \leq y \leq \frac{a}{2}$} \\
0, & \text{others}
\end{cases}
\]

1. 假定横线向右为正向，记投针与横线正向的角为\(\theta\)，则\(\theta \in[0, \pi]\),为均匀分布。

\[f(\theta) =
\begin{cases}
\frac{1}{\pi}, & \text{$0 \leq \theta \leq \pi$} \\
0, & \text{others}
\end{cases}
\]

投针与横线有交点，即\(y \leq \frac{L}{2}sin\theta\)

布丰投针估算\(\pi\) -- 蒙特卡罗模拟

针与横线有交点的概率：

\(P(x) = \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}f(y,\theta)dyd\theta = \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}f(y)f(\theta)dyd\theta \\
= \int_{0}^{\pi}\int_{0}^{\frac{L}{2}sin\theta}\frac{2}{a} * \frac{1}{\pi}dyd\theta = \frac{2L}{a\pi}\)

如果做n次投针实验，其中有k次针与横线相交，则针与横线相交的频率为：\(\frac{k}{n}\),根据大数定理，频率也就为概率。

$ \frac{2L}{a\pi} \approx \frac{k}{n}$ 即， \(\pi \approx \frac{2Ln}{ak}\)

MATLAB模拟实验

用布丰投针实验近似计算\(pi\)的值：

代码如下：

l = 0.6; %针的长度
a = 1; %平行线的宽度
n = 1000000; %做n次投针试验
k = 0; %记录针与平行线相交的次数
y = unifrnd(0, a/2, 1, n); %在[0, a/2]内服从均匀分布随机产生n个数
theta = unifrnd(0, pi, 1, n); %在[0, pi]内服从均匀分布随机产生n个数
for i=1:n
    if y(i) < (l/2)*sin(theta(i))
        k = k + 1;
    end
end
f = k / n;
Pi = (2*l*n)/(a*k);

结果如图所示：



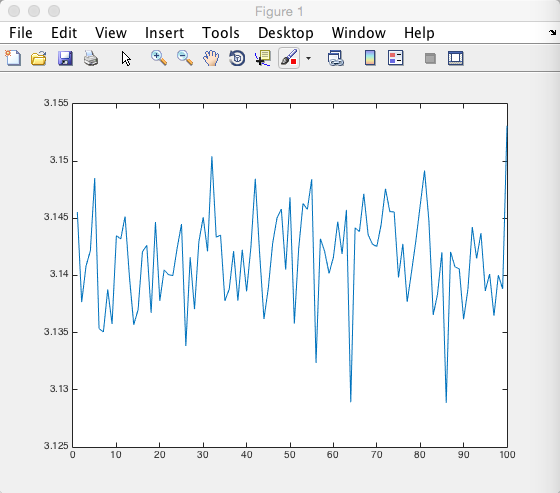
如此进行多次实验，进行估计。

如图为进行100次重复投针实验，每次投针1000000次，结果如图所示：