多分类问题multicalss classification

多分类问题：有N个类别C₁,C₂,...,C_n,多分类学习的基本思路是“拆解法”，即将多分类任务拆分为若干个而分类任务求解，最经典的拆分策略是：“一对一”，“一对多”，“多对多”

(1)一对一

给定数据集D={(x₁,y₁),(x₂,y₂),...,(x_n,y_n)},y_i€{c₁,c₂,...,c_N},一对一将这N个类别两两配对，从而产生N(N-1)/2个二分类任务，在测试阶段新样本将同时提交给所有的分类器，于是将得到N(n-1)/2个分类结果，最终把预测最多的结果作为投票结果。

算法：

（2）一对多

一对多则是将每一个样例作为正例，其他剩余的样例作为反例来训练N个分类器，如果在测试时仅有一个分类器产生了正例，则最终的结果为该分类器，如果产生了多个正例，则判断分类器的置信度，选择置信度大的分类别标记作为最终分类结果。

算法：

举例描述：

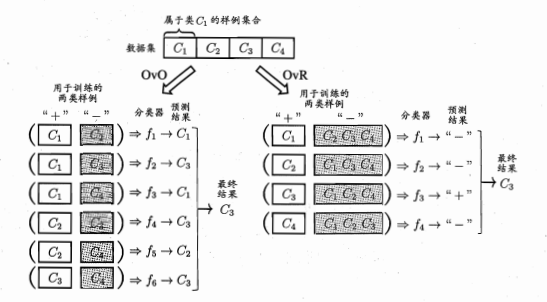
一对一问题：如果有4个类，首先从中任选两个类，进行标记，判断某一个样例更倾向于哪一个类，记录预测的结果，对所有的样例进行判断，看他应该属于两个类中的哪一个，然后选择其他的两个类，重复这个过程，最后收集某一个样例的全部判断结果，会得到不同的结果，找到其中的所占的比例最大的结果即为最终的结果。

（3）多对多问题：

有一种最常用的技术是：”纠错输出码“，分为两个阶段，编码阶段和解码阶段

编码阶段：对N个类别进行M次划分，每次将一部分类划分为正类，一部分类划分为反类，编码矩阵有两种形式：二元码和三元码，前者只有正类和反类，后者除了正类和和反类还有停用类，在解码阶段，各分类器的预测结果联合起来形成测试示例的编码，该编码与各类所对应的编码进行比较，将距离最小的编码所对应的类别作为预测结果。

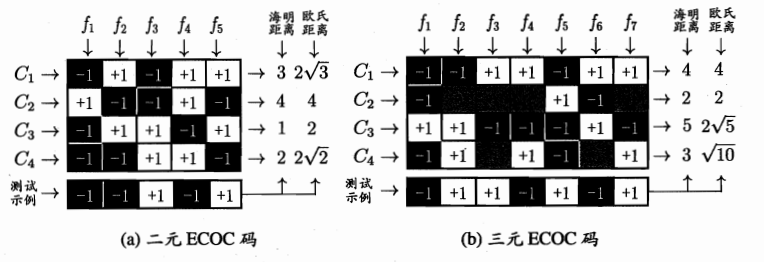
例如：在上图（1）中，f1分类器使得所有的C2为正例，其他为反例，f2分类器使得C1,C3为正，剩余分类器如图所示，因此可以得到一串输入码，以C1为例，其输入码为（-1，+1，-1，+1，+1）对于测试用例（-1，-1，+1，-1，+1）计算它与其他类的距离，即计算输入码和测试用例的欧式距离以C1和测试用例为例=(-1-1)²+(+1-1)²+(-1-1)²+(+1+1)²+(+1-1)²=12^½

海明距离：

计算海明距离的一种方法，就是对两个位串进行异或（xor）运算，并计算出异或运算结果中1的个数。例如110和011这两个位串，对它们进行异或运算，其结果是：

110⊕011=101

异或结果中含有两个1，因此110和011之间的汉明距离就等于2