生成1~n的全排列

输入正整数n,输出n的全排列。

样例输入1:

3

样例输出1：

1 2 3

1 3 2

2 1 3

2 3 1

3 1 2

3 2 1

分析：

按字典序从小到大的顺序输出所有的排列。

（字典序：两个序列的字典序大小关系等价于从头开始第一个不相同位置处的大小关系）

使用数组a保存排列中的数，集合s代表剩下的数。

则有

方法1：

1.伪代码：

int dfs(a,s,cur){//找到排列中的第cur个数字。

If （s==空） 输出这个排列;

else

取集合s中的元素i;

a[cur]=i  ;//存到a数组中

dfs(a,s,cur+1);

}

s集合可以省掉，直接用a来表示，如果i在a[1]~a[cur-1]中存在，则说明i已经使用，否则说明i在集合s中。

因为要从第一个数字开始找，所以首先调用dfs(1)  //cur=1

源代码：

#include<cstring>

using namespace std;

int a[100],s, n;;

void dfs(int cur){//函数没有返回值，所以类型为void

if (cur==n+1) {

for (int i=1;i<n;i++) cout<<a[i]<<" ";

cout<<a[n]<<endl;

s++;

}

else for (int i=1;i<=n;i++){

int ok=1;

for(int j=1;j<cur;j++)  //因为当前找第cur个数字，所以和前面已经找到的cur-1个数字比较

if(a[j]==i) ok=0;

if (ok){ a[cur]=i ;dfs(cur+1);}

}

}

int main(){

memset(a,0,sizeof(a));

cin>>n;

dfs(1);

cout<<s<<endl;

return 0;

}

思考：

（1）全局变量与局部变量；

比如a数组和变量n,s在main和dfs中都要用到，所以定义为全局变量，cur只在当前调用的函数中使用，所以定义为局部变量。

（2）函数没有返回值时如何处理。

　　函数没有返回值时，函数类型为void，可以没有return语句，也可以有，但其后没有表达式

return ;

2.

伪代码：

int dfs(cur){//已经找到cur个数字，准备找下一个。

If （s==空） 输出这个排列;

else

取集合s中的元素i;

a[cur+1]=i  ;//存到a数组中

dfs(cur+1);

}

初始时已经找到了0个数字，所以首先调用dfs(0)

 #include<iostream>
 #include<cstring>
 using namespace std;
 int a[],s=, n;
 void dfs(int cur){//函数没有返回值时类型为void
     if (cur==n) {
         for (int i=;i<n;i++) cout<<a[i]<<" ";
         cout<<a[n]<<endl;
         s++;
     }
     else
          for (int i=;i<=n;i++){
               int ok=;
               for(int j=;j<=cur;j++)
                     if(a[j]==i) ok=;
               if (ok){
                   a[cur+]=i;
                   dfs(cur+);
             }
           }
 }

//使用标记数组
#include<iostream>
#include<cstdio>
using namespace std;
int a[],f[] ;
int n;
void dfs(int cur){
    if (cur==n) {
        for (int i=;i<n;i++) printf("%d ",a[i]);
        printf("%d\n",a[n]);
        return ;
    }
    for (int i=;i<=n;i++)
        if (!f[i]){
            a[cur+]=i;
            f[i]=; //标记i已经使用
            dfs(cur+);
            f[i]=;

        }
}
int main(){
    scanf("%d",&n);
    for (int i=;i<=n;i++) f[i]=;//f初值为0
    dfs();
    return ;
}

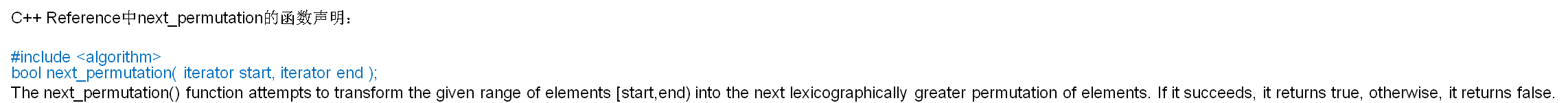
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
int a[],p[] ;
int n;
int main(){
    cin>>n;
    for (int i=;i<=n;i++) a[i]=i;//初值为最小的字母表顺序
    do{
        for (int i=;i<n;i++) printf("%d ",a[i]);
        printf("%d\n",a[n]);
    }while (next_permutation(a+,a+n+));
    return ;
}

参考网址：http://codevs.cn/problem/1294/

该题目卡cin，cout（第五个点过不了），使用scanf和printf就没有问题了。