LightOJ 1070 Algebraic Problem：矩阵快速幂 + 数学推导

题目链接：http://lightoj.com/volume_showproblem.php?problem=1070

题意：

　　给你a+b和ab的值，给定一个n，让你求a^n + b^n的值(MOD 2^64)。

题解：

　　a + b也就是a^1 + b^1，然后要从这儿一直推到a^n + b^n。

　　矩阵快速幂？o(￣▽￣)ｄ

　　那么主要解决的就是如何从a^n + b^n推到a^(n+1) + b^(n+1)。

　　下面是推导过程：

　　

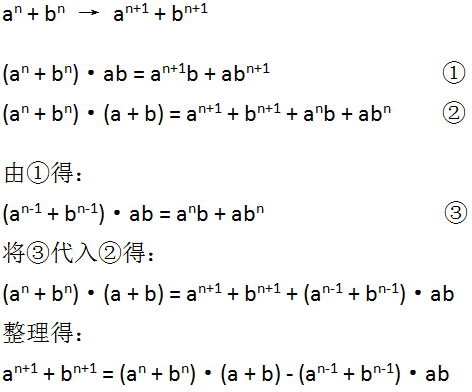
　　由于推a^(n+1) + b^(n+1)要用到a^n + b^n和a^(n-1) + b^(n-1)，所以初始矩阵为1*2大小，为[a^0+b^0, a^1+b^1]。

　　初始矩阵start：

　　

　　特殊矩阵special：

　　

　　所求矩阵ans：

　　ans = start * special^n

　　ans的第一项即为a^n + b^n.

　　注：由于题目要求MOD 2^64，所以直接将矩阵内元素定义为unsigned long long类型，自然溢出就好啦。

AC Code:

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #define MAX_L 5

 using namespace std;

 struct Mat
 {
     int n;
     int m;
     unsigned long long val[MAX_L][MAX_L];
     Mat()
     {
         n=;
         m=;
         memset(val,,sizeof(val));
     }
 };

 int p,q,n,t;

 Mat make_unit(int n)
 {
     Mat mat;
     mat.n=n;
     mat.m=n;
     for(int i=;i<n;i++)
     {
         mat.val[i][i]=;
     }
     return mat;
 }

 Mat make_start()
 {
     Mat mat;
     mat.n=;
     mat.m=;
     mat.val[][]=;
     mat.val[][]=p;
     return mat;
 }

 Mat make_special()
 {
     Mat mat;
     mat.n=;
     mat.m=;
     mat.val[][]=;
     mat.val[][]=-q;
     mat.val[][]=;
     mat.val[][]=p;
     return mat;
 }

 Mat mul_mat(const Mat &a,const Mat &b)
 {
     Mat c;
     if(a.m!=b.n)
     {
         cout<<"Error: mul_mat"<<endl;
         return c;
     }
     c.n=a.n;
     c.m=b.m;
     for(int i=;i<a.n;i++)
     {
         for(int j=;j<b.m;j++)
         {
             for(int k=;k<a.m;k++)
             {
                 c.val[i][j]+=a.val[i][k]*b.val[k][j];
             }
         }
     }
     return c;
 }

 Mat quick_pow_mat(Mat mat,long long k)
 {
     Mat ans;
     if(mat.n!=mat.m)
     {
         cout<<"Error: quick_pow_mat"<<endl;
         return ans;
     }
     ans=make_unit(mat.n);
     while(k)
     {
         if(k&)
         {
             ans=mul_mat(ans,mat);
         }
         mat=mul_mat(mat,mat);
         k>>=;
     }
     return ans;
 }

 int main()
 {
     cin>>t;
     for(int cas=;cas<=t;cas++)
     {
         cin>>p>>q>>n;
         Mat start=make_start();
         Mat special=make_special();
         Mat ans=mul_mat(start,quick_pow_mat(special,n));
         cout<<"Case "<<cas<<": "<<ans.val[][]<<endl;
     }
 }