【清华集训】小Y和地铁

图已挂，前往luogu

题目：

小 $\rm Y$ 是一个爱好旅行的 $\rm OIer$。一天，她来到了一个新的城市。由于不熟悉那里的交通系统，她选择了坐地铁。
她发现每条地铁线路可以看成平面上的一条曲线，不同线路的交点处一定会设有换乘站。通过调查得知，没有线路是环线，也没有线路与自身相交。任意两条不同的线路只会在若干个点上相交，没有重合的部分，且没有三线共点的情况。即，如图所示的情况都是不存在的：

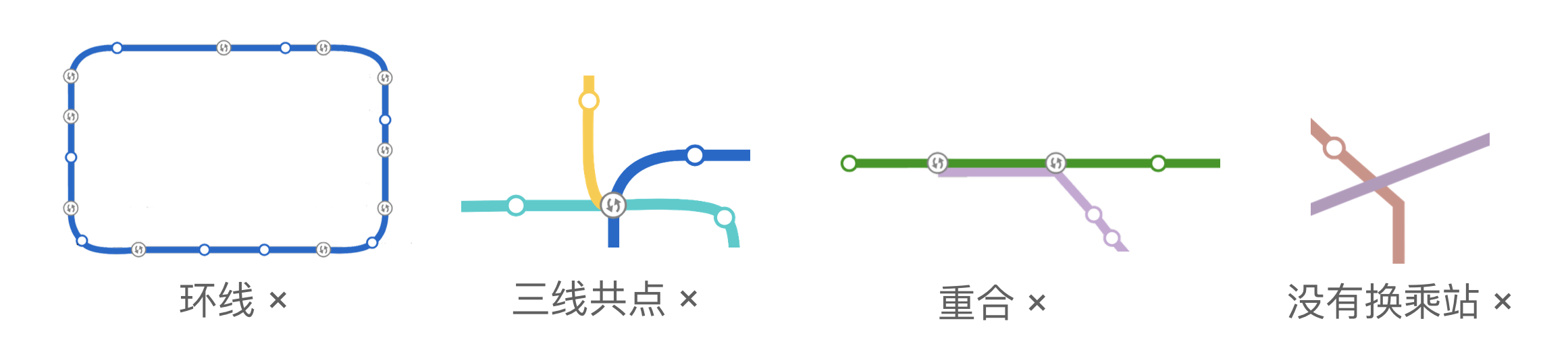
小 $\rm Y$ 坐着地铁 $0$ 号线，路上依次经过了 $n$ 个换乘站。她记下了每个换乘站可以换乘的线路编号，发现每条线路与她所乘坐的线路最多只有 $2$ 个换乘站。现在小 $\rm Y$ 想知道，除掉她经过的换乘站以外，这个城市里最少有几个换乘站。只有你告诉她正确的答案，她才会答应下次带你去玩呢。

$n\le 44$

分析：

首先，我们先考虑最暴力的方法：

我们发现，对于两个换乘站，共有$8$种情况：

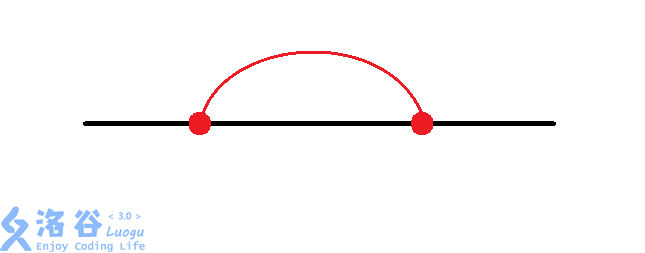
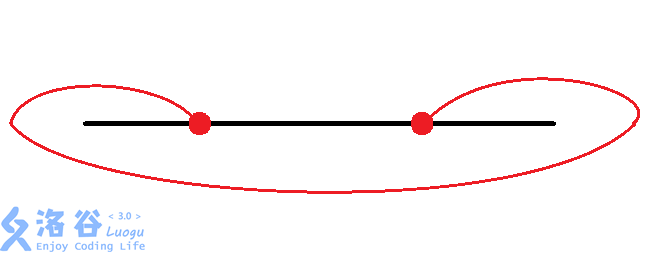
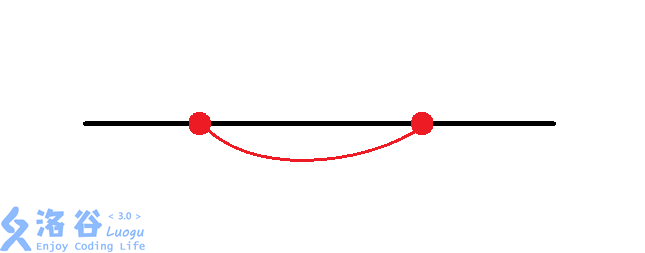
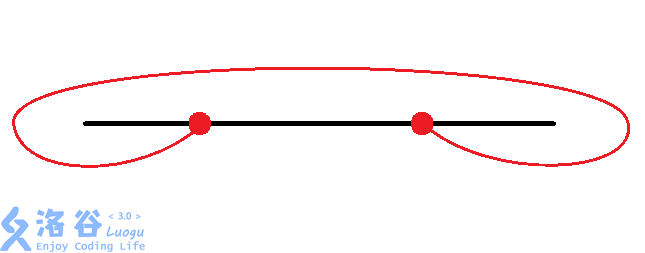
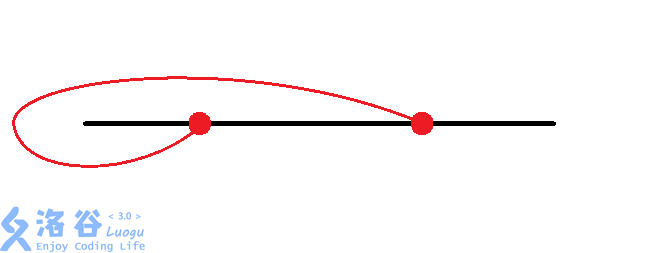
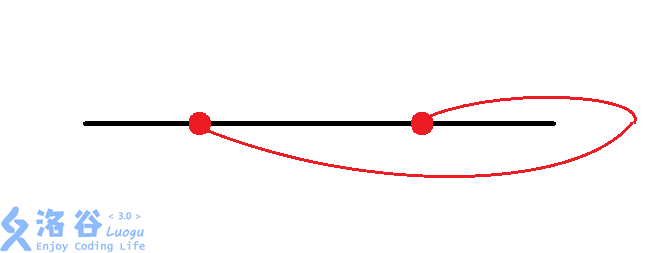
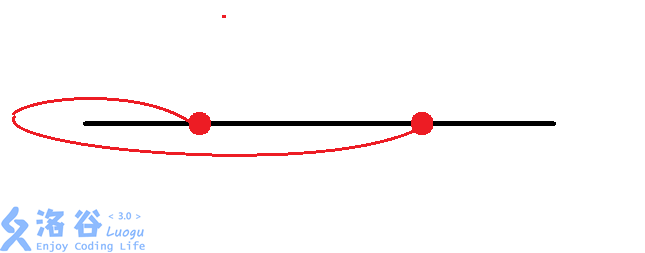
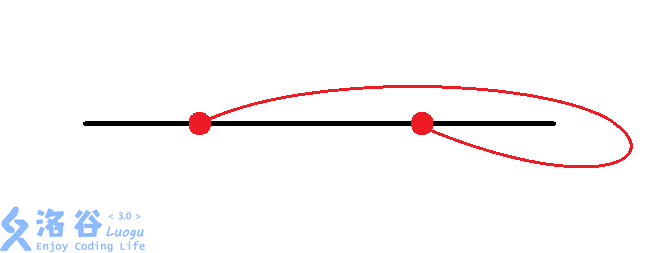
考虑我们对每组换乘站进行枚举，再加上$O(n)$的暴力找交点数，时间复杂度为$O(n8^\left(\frac{n}{2}\right))$，面对$n\le 44$的数据，显然会$\rm TLE$。

期望得分$\rm 10$。

考虑寻找这$8$种情况有没有重复。

我们发现，对于第一行的两种情况，放到一起，会是这样的：

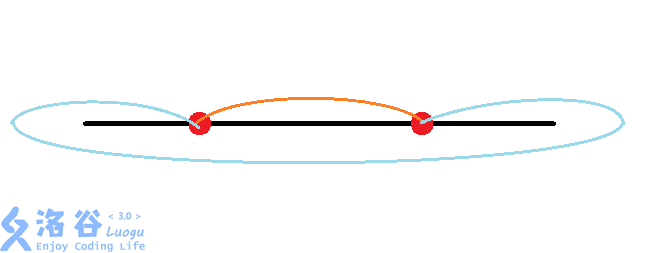
对于这种情况，由于这两条线产生了一个完全包住$0$号线的环，我们发现对于每一个其他的线，要么不和这两条线产生交点，要么对这两条线每条都产生一个交点。

所以，不管朝左还是朝右，结果都是一样的，我们只需要枚举朝上或朝下即可。

时间复杂度$O(n4^\left(\frac{n}{2}\right))$，期望得分$40$分。

再考虑，能不能继续减少情况数。

比如，我们把第一列的两种放到一起。

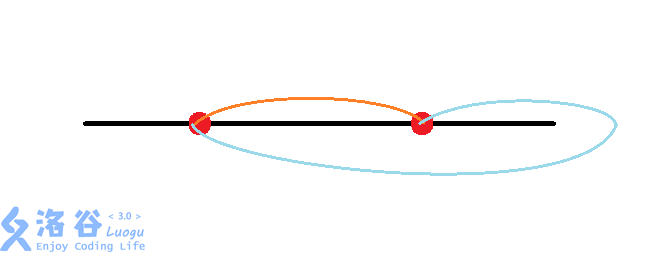
这张图也构成了环，但是这个环并没有能把0号线包住，但是这个环把0号线右边的所有点包住了，也就是在第一个红点右边的所有点是不会受到这两个的选择的影响的。

然后再来看第一个红点左边的情况，如果你是按左端点从左往右搜索的，你会发现到这步的时候红点左边已经搜索完了，即在左边会进出环的点已经全部决定了，而又因为不会对右边造成影响，所以我们可以贪心地取这两条环产生交点的最小值。

同理，剩下的也可以这样处理。

时间复杂度$O(n2^\left(\frac{n}{2}\right))$。

期望得分$\rm 80$分。

搜索的时间复杂度看上去已经很优了，所以我们考虑能不能优化找交点的时间复杂度。

考虑我们从左往搜索，用$a.l,a.r$表示$a$线路的左端点右端点，若只考虑同向，因为$a.l \lt a.r,\;b.l \lt b.r,\; a.l \lt b.l$则有三种情况：

$$1)\quad a.l\lt b.l\lt b.r \lt a.r$$

$$2)\quad a.l\lt a.r\lt b.l \lt b.r$$

$$3)\quad a.l\lt b.l \lt a.r \lt b.r$$

显然，只有情况$3$是相交的。

我们发现只有$b.l\lt a.r\lt b.r$我们才需要统计。

是不是很熟悉？你可以使用树状数组来进行统计。

每个右端点标记$1$，然后求$[b.l,b.r]$的和即可。

对于朝向问题，显然左端点的朝向不影响，右端点只有同向才会相交，可以自行画图，这边不作演示。

至于代码，由于写的时候比较早，太丑就不放出来了。

时间复杂度$O(2^{\left(\frac{n}{2}\right)}\log n)$，可以$\rm AC$。

有问题请留言。

后记：

$\rm hyc\;dalao$说这题是$\rm dfs$模板题，实在太强了。