xgboost算法原理

XGBoost是2014年3月陈天奇博士提出的，是基于CART树的一种boosting算法，XGBoost使用CART树有两点原因：对于分类问题，CART树的叶子结点对应的值是一个实际的分数，而非一个确定的类别，这有利于实现高效的优化算法；XGBoost有两个特点快和准，快一方面是并行的原因，另一方面是CART树的计算没有对数项。

XGBoost首先是一种基于决策树的集成模型，假设有K棵CART树，则集成的预测结果为：（fK代表第k颗树的输出结果）

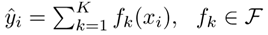
XGBoost的目标优化函数定义为：

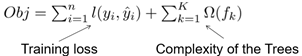
目标优化函数的第一项为训练损失，第二项为树模型的复杂度，也是优化函数的正则化项。Xgboost包含的CART树的确定包括两个部分：树的结构、叶子节点分数，如果树的结构确定，模型的正则化项也设为各个叶子节点值的平方和，就可以使用梯度下降或随机梯度下降来优化目标函数。

XGboost目标函数的优化采用的是加法训练，这是一种启发式算法，运用加法训练，首先优化第一棵树，之后再优化第二棵树，直至优化完k棵树。

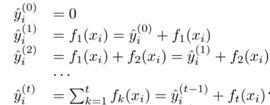
第t步时，在现有的t-1棵树的基础上，添加使目标函数最小的第t颗CART树：

对于平方损失函数，目标优化函数可表示为：

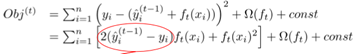
对于一般的损失函数，可以对目标函数做二阶泰勒展开，得到目标优化函数：

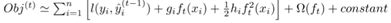
其中：

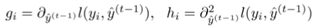
等价于平方损失函数中的：

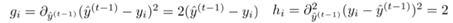
二阶泰勒展开形式：

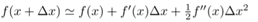
移除常数项后，得到的近似目标优化函数为：

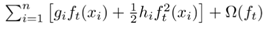
模型的正则化项定义为：

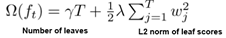
将正则化项代入目标优化函数得：

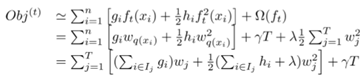
令：

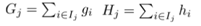
目标函数等价于：
   

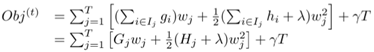
假设树的结构固定，优化每个叶子节点的权重，目标函数对wj求偏导等于0可得：

XGBoost的节点切分标准定义为：

该Gain实际上是单节点的obj减去切分后的两个子节点的obj，Gain为正，值得切分，Gain的左半部分大于g，值得切分。

Xgboost对样本的遍历转化成了在叶子节点上遍历，特征的选择和切分可以并行实现，优于传统的GBDT算法。