softmax回归---sigmoid（1）

介绍softmax之前先讲讲sigmoid：

逻辑回归模型常用的函数：sigmoid函数（用来做二分类）

• 表达式：f(x)=L/(1+exp^-k(x-x0))
• 其图像：
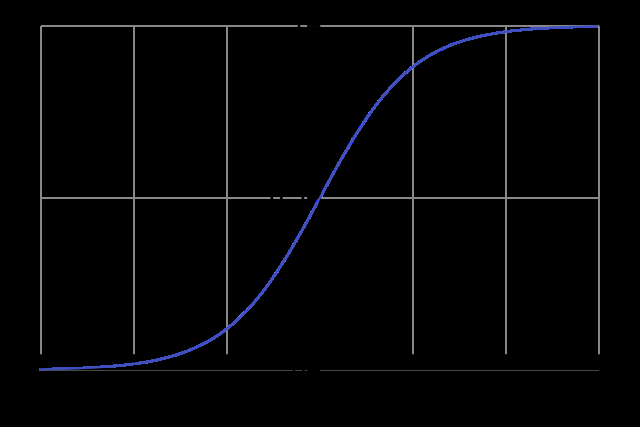
• 本质：将一个真值映射到（0，1)之间

---

softmax函数（用作多分类）

• 形式：

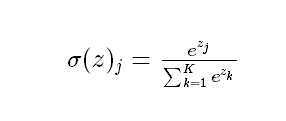
• 本质：把一个k维的向量映射为另一个K维向量（该向量元素都在0-1之间），然后可以根据每一个向量元素的大小进行多分类的任务。

---

来自链接（http://ufldl.stanford.edu/wiki/index.php/Softmax回归）

softmax回归是logistics回归在多分类问题上的推广，在多分类问题中，类标签y可以取两个以上的值。

Softmax回归模型对于诸如MNIST手写数字分类等问题是很有用的，该问题的目的是辨识10个不同的单个数字。Softmax回归是有监督的，不过后面也会介绍它与深度学习/无监督学习方法的结合。（译者注： MNIST 是一个手写数字识别库，由NYU 的Yann LeCun 等人维护。http://yann.lecun.com/exdb/mnist/

---

来自链接（https://www.cnblogs.com/yinheyi/p/6131262.html）