Partition（hdu4651）2013 Multi-University Training Contest 5----（整数拆分一）

Partition

Time Limit: 6000/3000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 954 Accepted Submission(s): 545

Problem Description

How many ways can the numbers 1 to 15 be added together to make 15? The technical term for what you are asking is the "number of partition" which is often called P(n). A partition of n is a collection of positive integers (not necessarily
distinct) whose sum equals n.



Now, I will give you a number n, and please tell me P(n) mod 1000000007.

Input

The first line contains a number T(1 ≤ T ≤ 100), which is the number of the case number. The next T lines, each line contains a number n(1 ≤ n ≤ 10⁵) you need to consider.

Output

For each n, output P(n) in a single line.

Sample Input

4
5
11
15
19

Sample Output

7
56
176
490

Source

field=problem&key=2013+Multi-University+Training+Contest+5&source=1&searchmode=source" target="_blank">2013 Multi-University Training Contest 5

题意：问一个数n能被拆分成多少种方法

首先你要知道母函数+然后你要知道五边形数定理；

设第n个五边形数为，那么，即序列为：1,
5, 12, 22, 35, 51, 70, ...

相应图形例如以下：

设五边形数的生成函数为。那么有：

以上是五边形数的情况。以下是关于五边形数定理的内容：

五边形数定理是一个由欧拉发现的数学定理。描写叙述欧拉函数展开式的特性。欧拉函数的展开式例如以下：

欧拉函数展开后，有些次方项被消去。仅仅留下次方项为1, 2, 5, 7, 12, ...的项次，留下来的次方恰为广义五边形数。

五边形数和切割函数的关系

欧拉函数的倒数是切割函数的母函数。亦即：

   当中为k的切割函数。

上式配合五边形数定理，有：

 

在 n>0 时，等式右側的系数均为0，比較等式二側的系数，可得

 

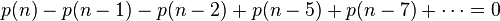
因此可得到切割函数p(n)的递归式：

比如n=10时，有：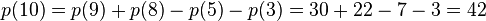

所以，通过上面递归式，我们能够非常高速地计算n的整数划分方案数p(n)了。

详见维基百科：https://zh.wikipedia.org/wiki/%E4%BA%94%E8%A7%92%E6%95%B0#.E5.BB.A3.E7.BE.A9.E4.BA.94.E9.82.8A.E5.BD.A2.E6.95.B8 或 https://zh.wikipedia.org/wiki/%E4%BA%94%E9%82%8A%E5%BD%A2%E6%95%B8%E5%AE%9A%E7%90%86 

转载请注明出处：http://blog.csdn.net/u010579068 

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=4651

详见代码：

#include<iostream>
#include<cstdio>
#define NN 100005
#define LL __int64
#define mod 1000000007

using namespace std;
LL wu[NN],pa[NN];
void init()
{
    pa[0]=1;
    pa[1]=1;
    pa[2]=2;
    pa[3]=3;
    LL ca=0;
    for(LL i=1;i<=100000/2;i++)
    {
        wu[ca++]=i*(3*i-1)/2;
        wu[ca++]=i*(3*i+1)/2;
        if(wu[ca-1]>100000) break;
    }
    for(LL i=4;i<=100000;i++)
    {
        pa[i]=(pa[i-1]+pa[i-2])%mod;
        ca=1;
        while(wu[2*ca]<=i)
        {
            if(ca&1)
            {
                pa[i]=(pa[i]-pa[i-wu[2*ca]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
                if(wu[2*ca+1]<=i)
                    pa[i]=(pa[i]-pa[i-wu[2*ca+1]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
            }
            else
            {
                pa[i]=(pa[i]+pa[i-wu[2*ca]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
                if(wu[2*ca+1]<=i)
                    pa[i]=(pa[i]+pa[i-wu[2*ca+1]])%mod;
                pa[i]=(pa[i]%mod+mod)%mod;
            }
            ca++;
        }
    }
}
int main()
{
    int T,n;
    init();
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        printf("%I64d\n",pa[n]);
    }
    return 0;

}