[jzoj 6092] [GDOI2019模拟2019.3.30] 附耳而至 解题报告 (平面图转对偶图+最小割)

题目链接：

https://jzoj.net/senior/#main/show/6092

题目：

知识点--平面图转对偶图

在求最小割的时候，我们可以把平面图转为对偶图，用最短路来求最小割，这样会比dinic更快，但只是只用于网格图

网格图(平面图),即满足可以画在平面，且任意两条边的交点只能是边的顶点的图

性质：一个联通的平面图有$n$个点，$m$条边，$f$个面，那么有$f=m-n+2$

对于一个平面图，我们可以找到它的对偶图。做法是把每一个分割出来的面作为一个个顶点，两个面之间存在边并且仅当这两个面在原图中存在公共边，新连的边的边权就是公共边的边权

如图为例

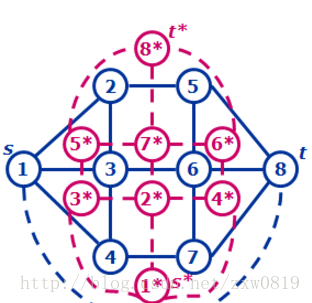
我们在下面找一个点$s*$，在上面找一个$t*$，在源点与汇点之间跑最短路即为原图的最小割。这个结论看起来蛮显然的

注意$s*$和$t*$要视情况而定来寻找(个人看法，我也没写过几道这样的题目，一般而言$dinic$优化一下就足够了)

那么如何把平面图转为对偶图呢？

我们对原图每一个点把连着它的边做极角排序。然后我们考虑一条边(有向)，强制让它顺时针或者逆时针方向(这个都可以，但是每一条边定义的方向是要一样的，接下来就按顺时针来叙述)，这样的话它的反向边就会朝另外一个方向，于是这样两个平面就建立起了双向边

其实最难的还是如何确定一个平面。设一条边起点为$u$，终点为$v$，这条边为$l$，做法是在顺时针转后在找到相对于v而言极角比l大的第一条边，很显然这样找到的边$r$和之前的边$l$就是同一个平面的两条相邻的边，那么我们就记下$nxt[l]=r$。弄完所有的边后，我们遍历每一条边并对取到的边标记，然后不断取$nxt$,知道取到又取到标记的边为止，这样我们就找到了一个面。口述比较难以理解，代码通俗易懂。值得注意的是这样我们也会把那个外面的无穷大平面找到

题解：

• 先把平面图转化为对偶图，在转化的过程中就可以算出每个平面的光明值和黑暗值，当然无限大的平面也可以算出
• 我们建一个超级源点S和一个超级汇点T，S向每个面连有向边，容量为其光明值，每个面向T连有向边，容量为其黑暗值。相邻的面之间连的是无向边，容量为其交边的c值
• 很显然答案为所有面的光明值和黑暗值之和减去这张图的最小割
• 归纳：这样每个元素有两个选择的很多都可以转化为最小割模型。并且由于最小割是最小化，若答案是最大化的化总是要用总的减去最小割的值（如最大权闭合子图模型）

代码：

#include<algorithm>
#include<cstring>
#include<iostream>
#include<cmath>
#include<cstdio>
#include<vector>
#include<queue>
using namespace std;
typedef long long ll;
typedef double db;

const int N=1e5+;
const int M=5e5+;
const ll inf=1e18;
int n,m;
inline char gc() {
    static char buf[],*p1,*p2;
    if (p1==p2) p1=(p2=buf)+fread(buf,,,stdin);
    return p1==p2?EOF:*p2++;
}
inline ll read()
{
    char ch=gc();ll s=,f=;
    while (ch<''||ch>'') {if (ch=='-') f=-;ch=gc();}
    while (ch>=''&&ch<='') {s=(s<<)+(s<<)+ch-'';ch=gc();}
    return s*f;
}
struct Point
{
    int x,y,a,b;
}p[N];
struct EDGE
{
    int u,v,c;
}edge[N<<];
vector <int> t[N];
bool cmp(int a,int b)
{
    int x1=p[edge[a].v].x-p[edge[a].u].x,y1=p[edge[a].v].y-p[edge[a].u].y;
    int x2=p[edge[b].v].x-p[edge[b].u].x,y2=p[edge[b].v].y-p[edge[b].u].y;
    return atan2((db)y1,(db)x1)<atan2((db)y2,(db)x2);
}
int tot;
int vis[M],nxt[M],bel[M];
ll gms[M],has[M];
int cnt=,T,S;
int head[M];
ll sum;
struct E
{
    int to,nxt;
    ll cap;
}e[M];
void adde(int u,int v,int c)
{
    e[++cnt]=(E){v,head[u],c};
    head[u]=cnt;
}
void insert(int u,int v,int c)
{
    adde(u,v,c);adde(v,u,);
}
void build()//平面图转对偶图
{
    for (int i=;i<=n;i++) sort(t[i].begin(),t[i].end(),cmp);
    for (int i=;i<(m<<);i++)
    {
        int v=edge[i].v;
        vector<int>::iterator it=++lower_bound(t[v].begin(),t[v].end(),i^,cmp);
        if (it==t[v].end()) it=t[v].begin();
        nxt[i]=*it;
    }
    for (int i=;i<(m<<);i++) if (!vis[i])
    {
        ++tot;
        for (int j=i;!vis[j];j=nxt[j]) vis[j]=,bel[j]=tot;
    }
    //网络流建图
    for (int i=;i<(m<<);i++)
    {
        int u=bel[i],v=bel[i^],c=edge[i].c;
        gms[u]+=1ll*p[edge[i].u].a;has[u]+=1ll*p[edge[i].u].b;
        if (u>v) continue;
        adde(u,v,c);adde(v,u,c);
    }
    S=tot+;T=tot+;
    for (int i=;i<=tot;i++)
    {
        sum+=gms[i]+has[i];
        insert(S,i,gms[i]);
        insert(i,T,has[i]);
    }
}
queue <int> q;
int dep[M];
int bfs()
{
    while (!q.empty()) q.pop();
    memset(dep,,sizeof(dep));
    dep[S]=;
    q.push(S);
    while (!q.empty())
    {
        int k=q.front();q.pop();
        for (int i=head[k];i;i=e[i].nxt)
        {
            int y=e[i].to;
            if (e[i].cap&&!dep[y])
            {
                dep[y]=dep[k]+;
                q.push(y);
            }
        }
    }
    return dep[T];
}
int cur[M];
ll dfs(int x,ll a)
{
    if (x==T||!a) return a;
    ll f,flow=;
    for (int &i=cur[x];i;i=e[i].nxt)
    {
        int y=e[i].to;
        if (dep[y]==dep[x]+&&(f=dfs(y,min(e[i].cap,a)))>)
        {
            flow+=f;
            a-=f;
            e[i].cap-=f;
            e[i^].cap+=f;
            if (!a) break;
        }
    }
    return flow;
}
ll dinic()
{
    ll res=;
    while (bfs())
    {
        memcpy(cur,head,sizeof(head));
        res+=dfs(S,inf);
    }
    return res;
}
int main()
{
    freopen("everfeel.in","r",stdin);
    freopen("everfeel.out","w",stdout);
    int NUM=read();
    n=read();m=read();
    for (int i=;i<=n;i++) p[i].x=read(),p[i].y=read(),p[i].a=read(),p[i].b=read();
    for (int i=;i<m;i++)
    {
        int u=read(),v=read(),c=read();
        edge[i<<]=(EDGE){u,v,c};edge[i<<|]=(EDGE){v,u,c};
        t[u].push_back(i<<);t[v].push_back(i<<|);
    }
    build();
    printf("%lld\n",sum-dinic());
    return ;
}