学习es6 setter/getter研究

1.背景

　　　在ES6中，我们对类的定义如下

 class Person {
     // 构造函数
     constructor (name) {
         // 属性初始化
         this.name = name;
     }

     // 成员方法
     sayName () {
         console.log(this.name);
     }

     // 静态方法
     static sayHi () {
         console.log("Hi~");
     }
 }

　　其实本质还是基于javascript原型链机制开发的语法糖

2. 深入setter/getter

2.1 setter/getter的调用执行时机

 class Person {
     constructor(name,age) {
         this.name = name;
         this.age = age;
     }

     set name(name) {
         console.log("setter");
         this.name = name;
     }

     get name() {
         console.log("getter");
         return this.name;
     }
 }    

发现上面的代码报错

/**
* 　　这是因为，在构造函数中执行this.name=name的时候，就会去调用set name，
* 　　在set name方法中，我们又执行this.name = name，进行无限递归，
* 　　最后导致栈溢出(RangeError)。
* */

我们稍作修改，让这个代码可以正常执行，达到我们想要的效果。

 // 针对上面的情况，稍作修改
 class Person {
     constructor(name,age) {
         this.name = name;// 执行这里 --- 1
         this.age = age;
     }

     set name(name) { // 进入到这里进行设置  -- 2
         console.log("setter");
         this._name = name;
     }

     get name() { // 在这里将对应的值返回 --- 3
         console.log("getter");
         return this._name;
     }

     sayName() { // 这里的调用，又从 1-2-3
         console.log(this.name);
     }
 }
 let p2 = new Person("lisi",22);
 console.log(p2);// 真实的属性是 age  _name   而不是name
 p2.sayName();
 console.log(p2._name);// 如果你访问的是 p2.name  最后会执行 1-3 这两个步骤，会打印出getter    

控制台结果如下：

/**
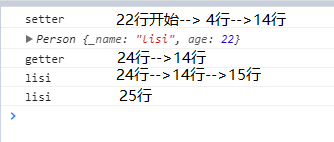
* 总结
* 　　 只要this.+属性名 和get 属性名/ set 属性名 中，属性名一致，
* 　　 this.name 会去调用getter 和 setter ，也就是说 getter和setter是hock函数
* 　　 而真实存储的属性是 _name 我们可以在实例化后，直接获取
* */

2.2 只有getter定义只读属性

 // 只有getter定义只读属性
 class foo {
     constructor(name) {
         this.name = name;
     }

     get name() {
         console.log(`getter函数`);
         return this.name;
     }
 }
 //Cannot set property name of #<foo> which has only a getter
  let p3 = new foo("李四");

/**
* 总结：
* 　　当一个属性只有getter没有setter的时候，我们是无法进行赋值操作的（第一次初始化也不行），这一点需要注意
* 　　当没有getter和setter时，就可以正常读写属性
* */