Resistance distance 图上2个节点的等效电阻求解算法

目录

• 如何计算正方体网络中(乃至更一般的图)2个节点间的等效电阻？ 公式的正确性很容易得到验证
• 如何计算Weighted matrix的Resistance matrix 我验证了特例，是对的，但是对直接计算出\(R\)没有什么用。等式右边有\(R\)，那你为什么不直接计算\(R^{-1}\)和\(det(R)\)
  • 论文1
    • 符号定义
    • 公式
  • 论文2
    • 符号定义
    • 公式
• 推荐阅读

如何计算正方体网络中(乃至更一般的图)2个节点间的等效电阻？ 公式的正确性很容易得到验证

物理学难题集萃原题。最高赞那个讲得很清楚了。纸笔算的话方法无非等位点法，对称电路方法及星三角变换方法等。

如果你想了解更加一般的通用解法，可以搜索Resistance distance

ResistanceDistance[g_Graph, i_Integer, j_Integer] :=
  Module[{n = VertexCount[g]},
   ResistanceDistanceMatix =
    PseudoInverse[KirchhoffMatrix[g] + 1/n*ConstantArray[1, {n, n}]];
   ResistanceDistanceMatix[[i, i]] + ResistanceDistanceMatix[[j, j]] -
     ResistanceDistanceMatix[[i, j]] -
    ResistanceDistanceMatix[[j, i]]];

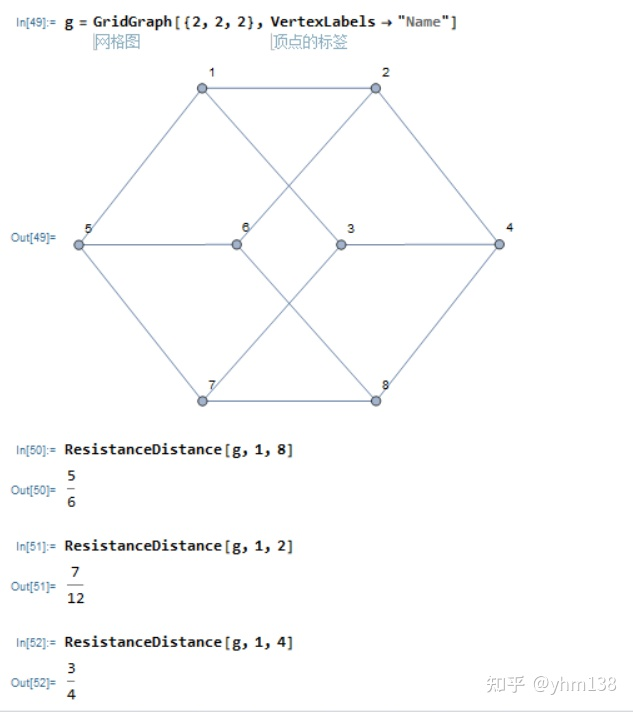
g = GridGraph[{2, 2, 2}, VertexLabels -> "Name"]
ResistanceDistance[g, 1, 8]
ResistanceDistance[g, 1, 4]
ResistanceDistance[g, 1, 2]

(*使用GraphData函数进行验证*)
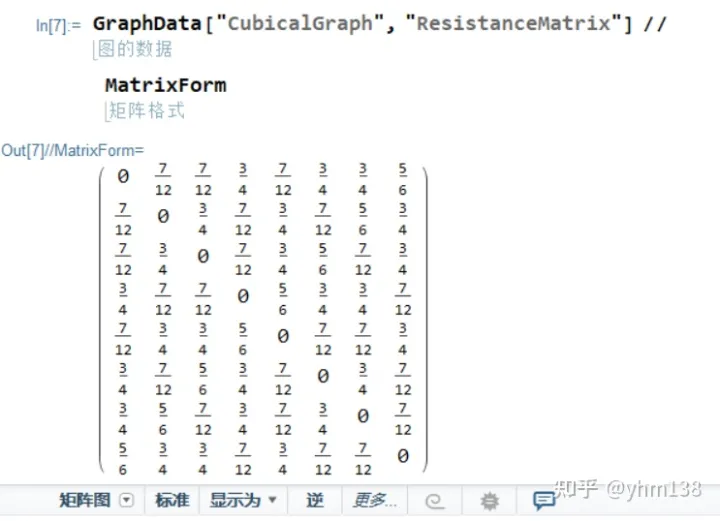
GraphData["CubicalGraph", "ResistanceMatrix"] // MatrixForm

(*不要指望拿GraphData函数计算任意一个边带权的图的电阻矩阵，emm查表查不出来的*)

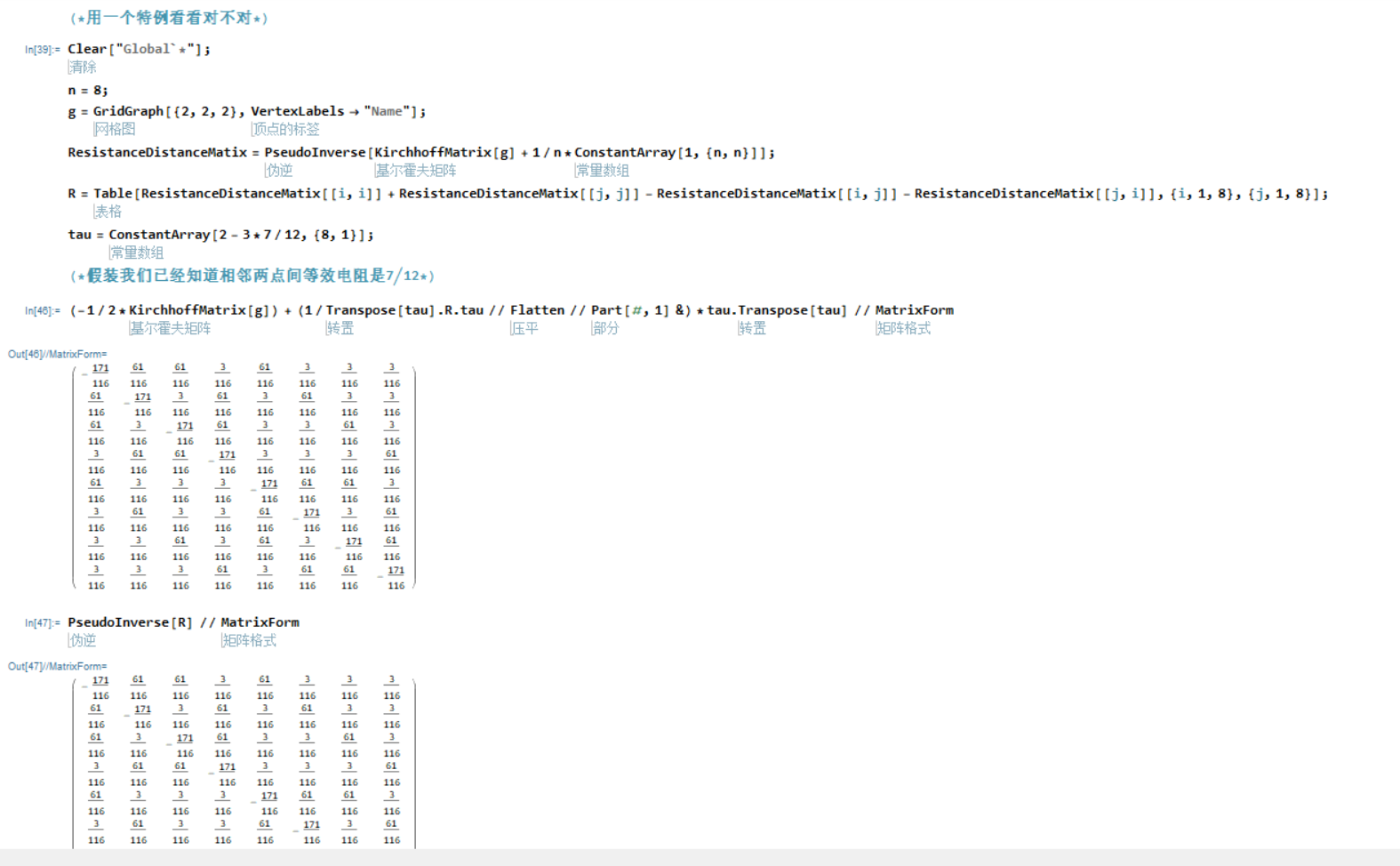
如何计算Weighted matrix的Resistance matrix 我验证了特例，是对的，但是对直接计算出\(R\)没有什么用。等式右边有\(R\)，那你为什么不直接计算\(R^{-1}\)和\(det(R)\)

你把它当成是只有\(R\)一个变量的矩阵方程来解，也几乎解不出来的啊

这里\(R\)的元素\(r(i,j)\)表示节点\(i\)和\(j\)之间的等效电阻。

或者你理解成这里的\(r(i,j)\)是ResistanceDistanceMatix经过

ResistanceDistanceMatix[[i, i]] + ResistanceDistanceMatix[[j, j]] - ResistanceDistanceMatix[[i, j]] - ResistanceDistanceMatix[[j, i]]]算出的结果，注意不要弄混了

论文1

边权重都是相同大小$s\times s$的正定矩阵，它的物理意义是什么？？？？？

Resistance matrices of graphs with matrix weights 这里考虑的边权重都是相同大小\(s\times s\)的正定矩阵  

符号定义

公式中符号的含义是：\(n\)是节点个数，边权重都是相同大小\(s\times s\)的正定矩阵，\(\operatorname{det}\)表示求行列式，\((.)^\prime\)表示求矩阵转置，\((.)^{-1}\)表示PseudoInverse伪逆，\(\chi(G)\)是\(L\)任意一个block的代数余子式(cofactor)

对于\(i,j=1,2,\cdots,n\)，定义\(n\times n\)的矩阵\(\tau_i\)满足 （ \(i\sim j\)表示\(i,j\)邻接）

\[\tau_i=2 I_s-\sum_{j \sim i} W_{i, j}^{-1} R_{j, i}
\]

定义\(ns\times s\)的矩阵\(\tau\)满足

\[\tau=\left[\tau_1, \tau_2, \cdots, \tau_n\right]^{\prime}
\]

拉普拉斯矩阵\(L\)的定义是：对于非对角线元素，如果\(i,j\)邻接，那么为\(-\frac{1}{w(i,j)}\)，否则是0；对于对角线元素，\(i\)行\(i\)列的元素是\(\sum\limits_{j\sim i}\frac{1}{w_{ij}}\)。矩阵\(L\)每一行的和是0.

公式

其中的Page 12,Theorem 4.1给出了\(R\)的行列式，公式如下：

\[\operatorname{det} R=(-1)^{(n-1) s} 2^{(n-3) s} \frac{\operatorname{det}\left(\tau^{\prime} R \tau\right)}{\chi(G)}
\]

其中的Page13,Theorem 4.2给出了\(R\)的逆，公式如下：

\[R^{-1}=-\frac{1}{2} L+\tau\left(\tau^{\prime} R \tau\right)^{-1} \tau^{\prime}
\]

论文2

Resistance matrix of a weighted graph 这里考虑的边权重都是正实数  

符号定义

公式中符号的含义是：\(n\)是节点个数，\(\operatorname{det}\)表示求行列式，\((.)^\prime\)表示求矩阵转置，\((.)^{-1}\)表示PseudoInverse伪逆，\(l(G)\)表示\(G\)的所有spannig tree的权重和。

对于\(i,j=1,2,\cdots,n\)，定义\(n\times 1\)的列向量\(\tau\)，其元素\(\tau_i\)满足 （ \(i \sim j\)表示\(i,j\)邻接）

\[\tau_i=2-\sum\limits_{j\sim i}\frac{r(i,j)}{w(i,j)}
\]

拉普拉斯矩阵\(L\)的定义是：对于非对角线元素，如果\(i,j\)邻接，那么为\(-\frac{1}{w(i,j)}\)，否则是0；对于对角线元素，\(i\)行\(i\)列的元素是\(\sum\limits_{j\sim i}\frac{1}{w_{ij}}\)。矩阵\(L\)每一行的和是0.

公式

其中的Page 7,Theorem 4给出了\(R\)的行列式，公式如下：

\[\operatorname{det} R=(-1)^{n-1} 2^{n-3} \frac{\tau^{\prime} R \tau}{l(G)}
\]

其中的Page 5,Theorem 3给出了\(R\)的逆，公式如下：

\[R^{-1}=-\frac{1}{2} L+\frac{1}{\tau^{\prime} R\tau} \tau \tau^{\prime}
\]

推荐阅读

https://en.wikipedia.org/wiki/Resistance_distance Resistance distance的维基百科词条