C++算法之旅、02 从木棒切割问题领悟二分法精髓

172、木棒切割问题

https://sunnywhy.com/problem/172

题目描述

给出n根木棒的长度，现在希望通过切割它们来得到至少k段长度相等的木棒（长度必须是整数），问这些长度相等的木棒的最大长度。

输入描述

第一行为两个正整数n、k（1≤n≤103、1≤k≤108），分别表示木棒的根数、需要得到的长度相等的木棒根数；

第二行为n个整数（1≤每个整数≤105），表示木棒的长度。

输出描述

一个整数，表示木棒的最大长度。如果无法达成，此时最大长度为0。

思考

如果通过暴力解法，那么复杂度为\(O(n^2)\)。每轮选择一个长度遍历每根绳子。

已知木棒分割的长度为正整数，且位于\([1,max(每根绳子的长度)]\)区间。当前为有序序列。求解至少k段长度相等木棒时，木棒的最大长度。

有序序列+求第一个满足某条件的元素的位置 => 二分法

已知木棒分割的长度序列从小到大，那么每个木棒长度对应的木棒段数序列从大到小。

那么求木棒的最大长度，实际上在求最后一个 >= k 的木棒段数此时的木棒长度 。

但二分法是求第一个满足某条件的元素位置，为什么呢？不妨先试着编写求最后一个满足某条件元素位置的二分法。

假定序列从小到大排列，可以很容易写出下面三种情况。但在测试过程中，往往会出现死循环或没有输出的现象。

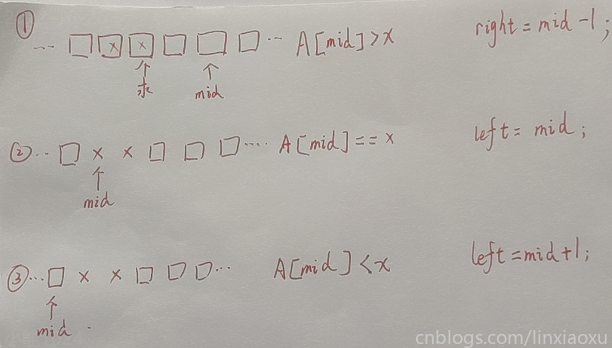
第1、3种情况无论如何也会让 \(left < right\) 不成立从而退出\(while\)循环。

那么很可能在第2种情况的时候陷入了死循环，求解一下死循环成立的条件。

\(\frac{left+right}{2} = left \\ \frac{right}{2} = \frac{left}{2} \\ \text 这是C语言的整除\)

二分法求解给定的\(while\)条件是\(left < right\)。显而易见，当left、right为相邻的奇偶时，且当 \(A[mid] == x\) 时，会无限死循环，每轮都会进入第2种情况。

所以牢记二分法用于寻找有序序列第一个满足某条件的元素的位置。

题解很简单，我们只需要求第一个分段数小于k的木棒长度然后减1即可。

解法

// https://sunnywhy.com/problem/172

// 考察二分查找

#define _CRT_SECURE_NO_WARNINGS
#include <cstdio>

int countSticks(int ans[], int len, int sep) {
    int total = 0;
    for (int i = 0; i < len; i++) {
        total += ans[i] / sep;
    }
    return total;
}

int main() {
    int n, k, ans[1010], max = 0;
    // 加载数据
    scanf("%d%d", &n, &k);
    for (int i = 0; i < n; i++) {
        scanf("%d", &ans[i]);
        if (ans[i] > max) {
            max = ans[i];
        }
    }
    // 逻辑处理
    int mid, left = 1, right = max;
    while (left < right) {
        mid = (left + right) / 2;
        if (countSticks(ans, n, mid) < k) {
            right = mid;
        } else {
            left = mid + 1;
        }
    };
    printf("%d\n", --left);

    return 0;
}

二分法固定模板