最大熵马尔科夫模型（MEMM）及其标签偏置问题

定义：

MEMM是这样的一个概率模型，即在给定的观察状态和前一状态的条件下，出现当前状态的概率。

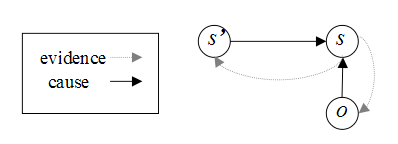
Ø  S表示状态的有限集合

Ø  O表示观察序列集合

Ø  Pr(s|s­­’,o):观察和状态转移概率矩阵

Ø  初始状态分布：Pr0(s)

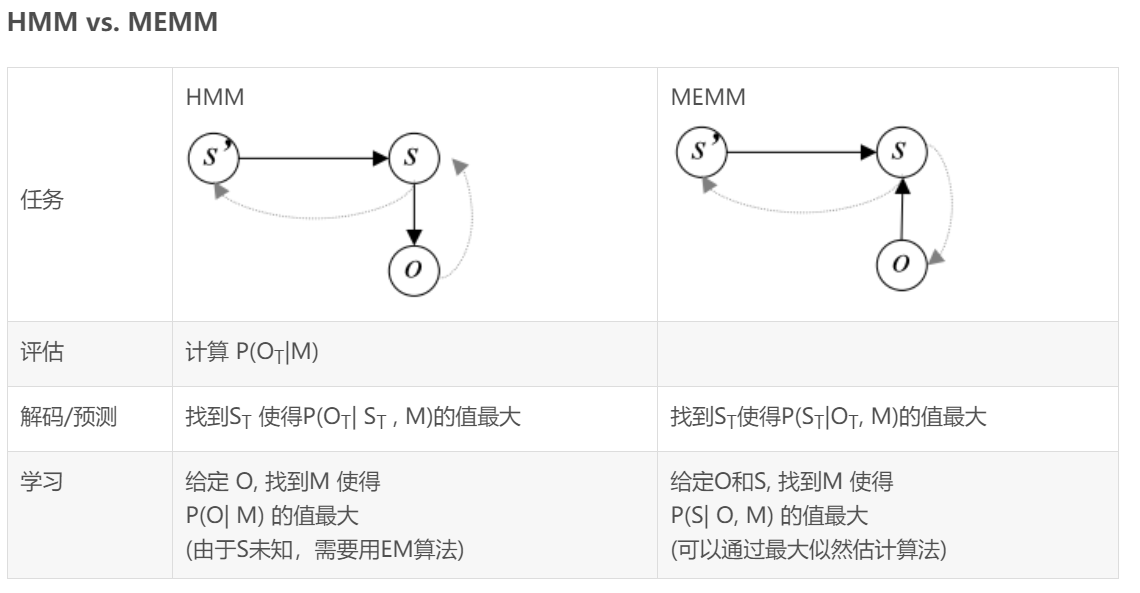
注：O表示观察集合，S表示状态集合，M表示模型

最大熵马尔科夫模型（MEMM）的缺点：

看下图，由观察状态O和隐藏状态S找到最有可能的S序列：

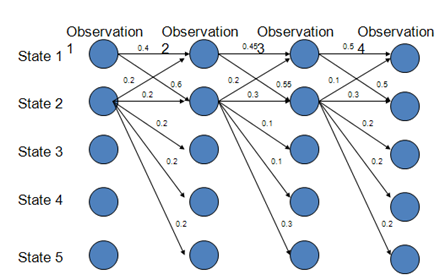
路径s1-s1-s1-s1的概率：0.4*0.45*0.5=0.09

路径s2-s2-s2-s2的概率: 0.2*0.3*0.3=0.018

路径s1-s2-s1-s2的概率: 0.6*0.2*0.5=0.06

路径s1-s1-s2-s2的概率: 0.4*0.55*0.3=0.066

由此可得最优路径为s1-s1-s1-s1

实际上，在上图中，状态1偏向于转移到状态2，而状态2总倾向于停留在状态2，这就是所谓的标注偏置问题，由于分支数不同，概率的分布不均衡，导致状态的转移存在不公平的情况。

由上面的两幅图可知，最大熵隐马尔科夫模型（MEMM）只能达到局部最优解，而不能达到全局最优解，因此MEMM虽然解决了HMM输出独立性假设的问题，但却存在标注偏置问题。

如图所示，“因为”是介词词性p,而 MEMM却错误标注其词性为连词c。产生该情况的原因正是一种偏置问题。

原因：“是”存在两个词性，动词v和代词r，包含在状态集合S1中；“因为”包括两个词性，介词p与连词c，包含在状态集合S2中；“事”只有一个词性，名词n，包含在状态集合S3中。由于MEMM对每个状态均定义一个指数模型，因此有：P(n|p)=1, P(n|c)=1, P(p|S1)+P(c|S1)=1; 基于马尔科夫假设，

P(S1, p, n)=P(p|S1)*P(n|p)=P(p|S1), 同理，P(S1, c, n)=P(c|S1)*P(n|c)=P(c|S1)。因此S2选择p节点还是c节点只取决于P(p|S1)、P(c|S1)，即只与“是”的上下文有关，与“因为”的上下文无关，这即使MEMM产生偏置的一种情况。