[2019HDU多校第五场][HDU 6626][C. geometric problem]

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6626

题目大意：给出平面上六个点\(A,B,M,N,X,Y\)以及两条直线\(L1,L2\)，要求在四边形\(ABNM\)内，直线\(L1\)上选一点\(S\)，在四边形\(XYNM\)内，直线\(L2\)上选一点\(T\)，使得\(S_{ASB}=S_{SMTN}=S_{XYT}\)

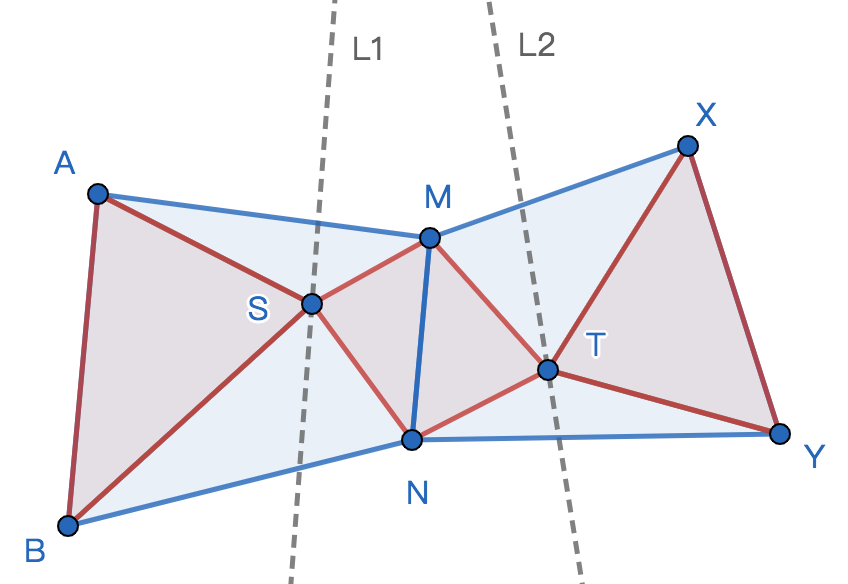
题解：设\(L1\)交\(ABNM\)于点\(P,Q\)，不妨设\(S=P+t\cdot (Q-P), 0\leq t \leq 1\)，则有$$2S_{ASB}=\vec{AB}\times \vec{AS}=\vec{AB}\times (\vec{AP}+t\cdot \vec{PQ})=\vec{AB}\times \vec{AP}+t\cdot \vec{AB}\times \vec{PQ}$$

　　　这个式子可以转换成为\(A+t\cdot B\)的形式。同理，三角形\(SMN,MNT,XYT\)均可以表示成这种形式，且\(ASB,SMN\)对应的\(t\)是\(S\)的坐标，不妨设为\(x\)，另外两个三角形对应的\(t\)则设为\(y\)。这样我们就能得到$$\left\{\begin{matrix}
2S_{ASB}=\vec{AB}\times \vec{AP}+x\cdot \vec{AB}\times \vec{PQ}\\
2S_{SMN}=\vec{MN}\times \vec{MP}+x\cdot \vec{MN}\times \vec{PQ}\\
2S_{MNT}=\vec{MN}\times \vec{MP'}+y\cdot \vec{MN}\times \vec{P'Q'}\\
2S_{XYT}=\vec{XY}\times \vec{XP'}+y\cdot \vec{XY}\times \vec{P'Q'}
\end{matrix}\right.$$

　　　根据题目要求，我们就能得出$$\left\{\begin{matrix}
2S_{ASB}-2S_{XYT}=\vec{AB}\times \vec{AP}-\vec{XY}\times \vec{XP'}+x\cdot \vec{AB}\times \vec{PQ}-y\cdot \vec{XY}\times \vec{P'Q'}=0\\
2S_{ASB}-2S_{SMN}-2S_{MNT}=\vec{AB}\times \vec{AP}-\vec{MN}\times \vec{MP}-\vec{MN}\times \vec{MP'}+x\cdot(\vec{AB}\times \vec{PQ}-\vec{MN}\times \vec{PQ})-y\cdot \vec{MN}\times \vec{P'Q'}=0
\end{matrix}\right.$$

　　　这是一个二元一次方程组，当然我们也可以将其当成两条直线的标准式来看，求出他们的交点就能得出对应的答案了。

　　　这里要注意，这里求出来的表达式可能不会有对应的直线（比如\(0\cdot x+0\cdot y=c \neq 0\)），或者会出现两直线没有交点，重合等情况，需要进行特判。另外还需要注意\(x,y\)解出来的值必须在\([0,1]\)这个范围内，否则也是无解。

　　　另外，由于这题要求在多解时输出字典序最小的解，所以在我们求交点的时候就可以让点\(P\)的字典序比\(Q\)小，这样只要尽量让\(x,y\)取到最小值就好了

　　　由于为了防止爆精度，看到坐标范围较小，想练习手写分数运算等种种原因，这题我除了输出外都是纯整数运算，不用担心爆精度了以后感觉改代码都方便了许多（指不需要调\(eps\)←_←）

#include<bits/stdc++.h>
using namespace std;
struct Frac
{
    long long p,q;
    void read(){q=,scanf("%lld",&p);}
    void simp()
      {int d=abs(__gcd(p,q));
      p/=d,q/=d;
      if(q<)p*=-,q*=-;
      if(p==)q=abs(q);
      }
    Frac operator +(const Frac &t)const
      {
      Frac res={p*t.q+t.p*q,q*t.q};
      res.simp();return res;
      }
    Frac operator -(const Frac &t)const
      {
      Frac res={p*t.q-t.p*q,q*t.q};
      res.simp();return res;
      }
    Frac operator *(const Frac &t)const
      {
      Frac res={p*t.p,q*t.q};
      res.simp();return res;
      }
    Frac operator /(const Frac &t)const
      {
      Frac res={p*t.q,q*t.p};
      res.simp();return res;
      }
    bool operator <(const Frac &t)const
      {
      return p*t.q<q*t.p;
      }
    bool operator ==(const Frac &t)const
      {
      return p==t.p && q==t.q;
      }
    void print(){printf("%.12f",1.0*p/q);}
};
int sgn(Frac k)
{
    if(k.p>)return ;
    if(k.p<)return -;
    return ;
}
struct Point
{
    Frac x,y;
    void read(){x.read(),y.read();}
    Point operator +(const Point &t)const{return {x+t.x,y+t.y};}
    Point operator -(const Point &t)const{return {x-t.x,y-t.y};}
    Frac operator *(const Point &t)const{return x*t.y-y*t.x;}
    Point operator *(const Frac &t)const{return {x*t,y*t};}
    Point operator /(const Frac &t)const{return {x/t,y/t};}
    bool operator <(const Point &t)const{return x==t.x?y<t.y:x<t.x;}
    bool operator ==(const Point &t)const{return x==t.x && y==t.y;}
    void print(){x.print(),putchar(' '),y.print();}
    bool check()
      {
      if(sgn(x)< || sgn(y)<)return false;
      if((Frac){,}<x || (Frac){,}<y)return false;
      return true;
      }
}A,B,M,N,X,Y,f[],g[],ans[];
struct Line
{
    Point p1,p2;
    void read(){p1.read(),p2.read();}
    bool check_isct(const Point &A,const Point &B)const
      {return sgn((p2-p1)*(A-p1))*sgn((p2-p1)*(B-p1))<=;}
    Point isct_Point(const Line &t)const
      {
      Frac a=(p2-p1)*(t.p1-p1);
      Frac b=(p2-p1)*(p1-t.p2);
      return (t.p1*b+t.p2*a)/(a+b);
      }
}L1,L2;
struct Line_Standard
{
    Frac A,B,C;
    bool check(){return sgn(A) || sgn(B) || !sgn(C);}
    bool check_isct(const Line_Standard &t)const
      {
      Frac tmp=A*t.B-B*t.A;
      if(sgn(tmp))return true;
      return sgn(C*t.B-B*t.C)==;
      }
    Point isct_Point(const Line_Standard &t)const
      {
      Frac tmp=A*t.B-B*t.A;
      if(!sgn(tmp))
        {
        if(sgn(C)==)return {{,},{,}};
        if(sgn(B)==)return {{,},{,}};
        if(sgn(A)==)return {{,},{,}};
        }
      return {(B*t.C-C*t.B)/tmp,(C*t.A-A*t.C)/tmp};
      }
    void print()
      {
      A.print(),putchar(' ');
      B.print(),putchar(' ');
      C.print(),putchar('\n');
      }
}h1,h2;
int T,cnt;
void rua(const Line &L,const Point &A,const Point &B,const int &lim)
{
    if(L.check_isct(A,B) && sgn((L.p2-L.p1)*(A-B)) && cnt<lim)
      if(!(L.isct_Point({A,B})==f[cnt]) || cnt==lim-)
        f[++cnt]=L.isct_Point({A,B});
}
void cal(const Point &A,const Point &B,const Point &C,const Point &D)
{
    Frac st=(B-A)*(C-A);
    Frac delta=(B-A)*(D-C);
    Frac ed=(B-A)*(D-A);
    if(sgn(st)< || sgn(ed)<)
      st.p=-st.p,delta.p=-delta.p;
    g[++cnt]={st,delta};
}
void print(const Point &P)
{
    Point S=f[]+(f[]-f[])*P.x;
    Point T=f[]+(f[]-f[])*P.y;
    S.print(),putchar(' ');
    T.print(),putchar('\n');
}
void init()
{
    cnt=;
    A.read(),B.read();
    M.read(),N.read();
    X.read(),Y.read();
    L1.read(),L2.read();
    rua(L1,A,B,),rua(L1,B,N,);
    rua(L1,N,M,),rua(L1,M,A,);
    rua(L2,X,Y,),rua(L2,Y,N,);
    rua(L2,N,M,),rua(L2,M,X,);
    if(f[]<f[])swap(f[],f[]);
    if(f[]<f[])swap(f[],f[]);
    cnt=;
    cal(A,B,f[],f[]);
    cal(M,N,f[],f[]);
    cal(M,N,f[],f[]);
    cal(X,Y,f[],f[]);
    h1={g[].y,(Frac){,}-g[].y,g[].x-g[].x};
    h2={g[].y-g[].y,(Frac){,}-g[].y,g[].x-g[].x-g[].x};
    if(!h1.check() || !h2.check())
      {printf("-1\n");return;}
    cnt=;
    Frac tmp=h1.A*h2.B-h1.B*h2.A;
    if(sgn(tmp)==)
      {
      if(sgn(h1.C*h2.B-h1.B*h2.C))
        {printf("-1\n");return;}
      if(!sgn(h1.A) && !sgn(h1.B))
        swap(h1,h2);
      if(h1.check_isct({{,},{,},{,}}))
        ans[++cnt]=h1.isct_Point({{,},{,},{,}});
      if(h1.check_isct({{,},{,},{,}}))
        ans[++cnt]=h1.isct_Point({{,},{,},{,}});
      if(h1.check_isct({{,},{,},{-,}}))
        ans[++cnt]=h1.isct_Point({{,},{,},{-,}});
      if(h1.check_isct({{,},{,},{-,}}))
        ans[++cnt]=h1.isct_Point({{,},{,},{-,}});
      for(int i=;i<=cnt;i++)
        if(ans[i].check())
          {print(ans[i]);return;}
      printf("-1\n");
      return;
      }
    ans[++cnt]=h1.isct_Point(h2);
    if(ans[].check())
      {print(ans[]);return;}
    printf("-1\n");
}
int main()
{
    scanf("%d",&T);
    while(T--)init();
}