OpenCV图像旋转

图像旋转是指图像按照某个位置转动一定角度的过程，旋转中图像仍保持这原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换，因此需要对图像旋转中的坐标进行相应转换。

如下图：

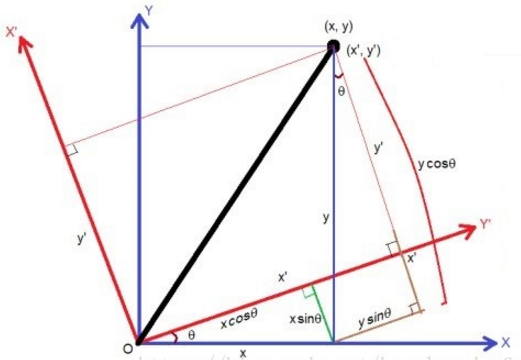
假设图像逆时针旋转\(\theta\)，则根据坐标转换可得旋转转换为：

\[ \begin{cases}
x' = r\cos(\alpha - \theta)\\
y' = r\sin(\alpha - \theta)\tag{1}
\end{cases}\]

而

\[r = \sqrt{x^2 + y^2},
\sin\alpha = \frac{y}{\sqrt{x^2 + y^2}},
\cos\alpha = \frac{x}{\sqrt{x^2 + y^2}}\]

带入(1)可得：

\[ \begin{cases}
x' = x\cos\theta + y\sin\theta\\
y' = -x\sin\theta + y\cos\theta
\end{cases}\]

即如下：

\[ \begin{bmatrix}
x'&y'& 1
\end{bmatrix} \
=
\begin{bmatrix}
x &y &1
\end{bmatrix} \
\begin{bmatrix}
\cos\theta & -\sin\theta & 0 \\
\sin\theta & \cos\theta &0 \\
0 & 0 & 1\tag{2}
\end{bmatrix}\]

而旋转后的图片的灰度值等于原图中相应位置的灰度值如下：

\[f(x', y') = f(x, y)
\]

同时我们要修正原点的位置，因为图像中的坐标原点在图像的左上角，经过旋转后图像的大小会有所变化，原点也需要修正。实现代码如下：

#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
#include <iostream>
#include <string>
#include <cmath>

using namespace cv;

Mat imgRotate(Mat matSrc, float angle, bool direction)
{
	float theta = angle * CV_PI / 180.0;
	int nRowsSrc = matSrc.rows;
	int nColsSrc = matSrc.cols;
	// 如果是顺时针旋转
	if (!direction)
		theta = 2 * CV_PI - theta;
	// 全部以逆时针旋转来计算
	// 逆时针旋转矩阵
	float matRotate[3][3]{
		{std::cos(theta), -std::sin(theta), 0},
		{std::sin(theta), std::cos(theta), 0 },
		{0, 0, 1}
	};
	float pt[3][2]{
		{ 0, nRowsSrc },
		{nColsSrc, nRowsSrc},
		{nColsSrc, 0}
	};
	for (int i = 0; i < 3; i++)
	{
		float x = pt[i][0] * matRotate[0][0] + pt[i][1] * matRotate[1][0];
		float y = pt[i][0] * matRotate[0][1] + pt[i][1] * matRotate[1][1];
		pt[i][0] = x;
		pt[i][1] = y;
	}
	// 计算出旋转后图像的极值点和尺寸
	float fMin_x = min(min(min(pt[0][0], pt[1][0]), pt[2][0]), (float)0.0);
	float fMin_y = min(min(min(pt[0][1], pt[1][1]), pt[2][1]), (float)0.0);
	float fMax_x = max(max(max(pt[0][0], pt[1][0]), pt[2][0]), (float)0.0);
	float fMax_y = max(max(max(pt[0][1], pt[1][1]), pt[2][1]), (float)0.0);
	int nRows = cvRound(fMax_y - fMin_y + 0.5) + 1;
	int nCols = cvRound(fMax_x - fMin_x + 0.5) + 1;
	int nMin_x = cvRound(fMin_x + 0.5);
	int nMin_y = cvRound(fMin_y + 0.5);
	// 拷贝输出图像
	Mat matRet(nRows, nCols, matSrc.type(), Scalar(0));
	for (int j = 0; j < nRows; j++)
	{
		for (int i = 0; i < nCols; i++)
		{
			// 计算出输出图像在原图像中的对应点的坐标，然后复制该坐标的灰度值
			// 因为是逆时针转换，所以这里映射到原图像的时候可以看成是，输出图像
			// 到顺时针旋转到原图像的，而顺时针旋转矩阵刚好是逆时针旋转矩阵的转置
			// 同时还要考虑到要把旋转后的图像的左上角移动到坐标原点。
			int x = (i + nMin_x) * matRotate[0][0] + (j + nMin_y) * matRotate[0][1];
			int y = (i + nMin_x) * matRotate[1][0] + (j + nMin_y) * matRotate[1][1];
			if (x >= 0 && x < nColsSrc && y >= 0 && y < nRowsSrc)
			{
				matRet.at<Vec3b>(j, i) = matSrc.at<Vec3b>(y, x);
			}
		}
	}
	return matRet;
}

测试代码：

 int main()
 {
 	std::string strPath = "D:\\MyDocuments\\My Pictures\\OpenCV\\";
 	Mat matSrc = imread(strPath + "panda.jpg");
 	if (matSrc.empty())
 		return 1;
 	float angle = 30;
 	Mat matRet = imgRotate(matSrc, angle, true);
 	imshow("src", matSrc);
 	imshow("rotate", matRet);
 	// 保存图像
 	imwrite(strPath + "rotate_panda.jpg", matRet);

 	waitKey();
 	return 0;
 }