2018-2019 ACM-ICPC, Asia Jiaozuo Regional Contest

Contest Info
Solutions

Contest Info

Solved	A	B	C	D	E	F	G	H	I	J	K	L
7/12	O	-	O	O	O	-	O	O	-	-	Ø	-

O 在比赛中通过
Ø 赛后通过
! 尝试了但是失败了
- 没有尝试

Solutions

A. Xu Xiake in Henan Province

签到。

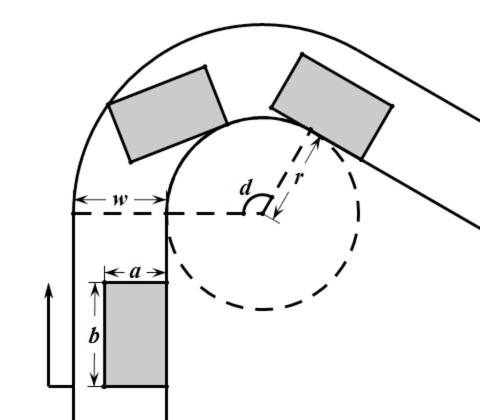
D. Keiichi Tsuchiya the Drift King

题意：
给出$a, b, r, d$，求最小的$w$。

E. Resistors in Parallel

题意：
给出$n$个电阻，第$i$个电阻的阻值为$：

$i$没有平方因子，阻值为$i$
$i$有平方因子，阻值为$\infty$

现有$n$个集合，第$i$个集合的编号为$i$，所有编号为$j(j \;|\; i)$的电阻都属于集合$i$。
一个集合的阻值为集合中所有电阻并联的电阻。
现在问阻值最小的集合是多少。

思路：
显然无穷大的电阻是没用的。
那么考虑答案集合为$x$，那么该集合的阻值为：
\[
\begin{eqnarray*}
R = \frac{1}{\sum\limits \frac{1}{R_j}}
\end{eqnarray*}
\]
其中$j \;|\; i$。
那么考虑变换式子，有：
\[
\begin{eqnarray*}
R = \frac{1}{\sum\limits \frac{\left\lfloor x / R_j \right\rfloor}{x}}
\end{eqnarray*}
\]
那么就是：
\[
\begin{eqnarray*}
R = \frac{x}{\sum\limits_{R_j}}
\end{eqnarray*}
\]
那么只需要求$x$的因子和就可以了。

F. Honeycomb

题意：
给出恶心的蜂房，求$S$到$T$最小经过多少个房间。

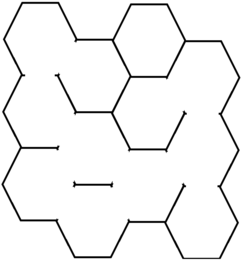
思路：
找规律模拟即可。

H. Can You Solve the Harder Problem?

题意：
给出$n$个数，每个数的值域为$[1, 10^6]$，现在要求所有本质不同的连续子区间的最大值的和。

思路：
本质不同，可以想到先进行后缀排序，然后考虑当前后缀的开头固定，结尾是一段连续的区间。
再考虑在原序列中，每个点向它后面的第一个比它大的数连边，那么会形成一棵森林。
那么对于每段后缀$i$，假设它的可选结尾范围为$[l_i, r_i]$，那么我们先找到$[i, l_i - 1]$这段范围最大的数的下标，然后看这个数的父亲$nx$。
那么我们发现结尾$[l_i, nx]$这段的最大值都是这个数。
然后后面的，就是树上一段到根的连续的东西，令边权为两个坐标相差的距离，那么每个点掌控的范围就是它到它父亲之间的那些点。
预处理一下贡献的前缀和，然后就可以$O(1)$计算了。

I. Distance

题意：
在一维数轴上给出$n$个点，告诉你$i \rightarrow i + 1$之间的距离，现在要求对于$k \in [1, n]$，回答选出$k$个点，使得所有的两两之间的距离和最大是多少

思路：
显然是两边轮着选，然后找规律统计下答案即可。

K. Counting Failures on a Trie

题意：
给出一个$Trie$，然后定义一种新的匹配规则：

一直在$Trie$上匹配，如果失配了，那么跳过这个字符并且从$Trie$的根开始匹配，并且失配次数$+1$。
那么每次匹配会得到失配次数，以及最终在$Trie$上匹配的末节点
现在给出一个字符串$S$，每次询问一段子串$S[l, r]$的失配次数以及最后匹配的末节点。

思路：
先将$Trie$的每个前缀都$Hash$然后将节点作为第二关键字存入$map$。
然后对于字符串$S$，处理一个倍增数组$f[i][j]$表示从$i$开始匹配$2^j$次最远能匹配到哪里。
然后对于每次询问，以$l$作为起点进行倍增即可找到最后一次匹配的开始节点$nl$。
那么就可以得到失配次数，那么最后的结点就是$S[nl, r]$这一段的$Hash$值在$mp$上的第二关键字。