剑指Offer-60~68题
60. \(n\) 个骰子的点数
题目描述：
扔 \(n\) 个骰子，向上面的数字之和为 \(S\)。给定 \(n\)，请列出所有可能的 \(S\) 值及其相应的概率。
示例：
输入：n = 1
输出：[[1, 0.17], [2, 0.17], [3, 0.17], [4, 0.17], [5, 0.17], [6, 0.17]]
解释：掷一次骰子，向上的数字和可能为1,2,3,4,5,6，出现的概率均为 0.17。
输入：n = 2
输出：[[2,0.03],[3,0.06],[4,0.08],[5,0.11],[6,0.14],[7,0.17],[8,0.14],[9,0.11],[10,0.08],[11,0.06],[12,0.03]]
解释：掷两次骰子，向上的数字和可能在[2,12]，出现的概率是不同的。
注意：
你不需要关心结果的准确性，我们会帮你输出结果。
思路：
动态规划。设 \(dp[i][j]\) 为前 \(i\) 个骰子数字和为 \(j\) 的次数，则 \(dp[i][j] = \sum_{k=1}^6dp[i-1][j-k]\)。
public class Solution {
/**
* @param n an integer
* @return a list of Map.Entry<sum, probability>
*/
public List<Map.Entry<Integer, Double>> dicesSum(int n) {
// Write your code here
// Ps. new AbstractMap.SimpleEntry<Integer, Double>(sum, pro)
// to create the pair
//n 个骰子点数和的最大数
final int maxNum = 6 * n;
//必须用 long，要不然可能溢出
long[][] dp = new long[n + 1][maxNum + 1];
for(int i = 1; i <= 6; i++) {
dp[1][i] = 1;
}
for(int i = 2; i <= n; i++) {
//前 i 个骰子点数和的最小数为 i， 最大数为 6*i
for(int j = i; j <= i * 6; j++) {
//k 要小于 j，例如：dp[2][2] 没有 k 为 2-6 的情况
for(int k = 1; k <= 6 && k < j; k++) {
dp[i][j] += dp[i-1][j-k];
}
}
}
//sum 为扔 n 个骰子的结果的总体次数
double sum = Math.pow(6, n);
List<Map.Entry<Integer, Double>> ret = new ArrayList<>();
for(int i = n; i <= maxNum; i++) {
//计算每个数值的概率
ret.add(new HashMap.SimpleEntry<>(i, dp[n][i] / sum));
}
return ret;
}
}
61. 扑克牌顺子
题目描述：
LL 今天心情特别好，因为他去买了一副扑克牌，发现里面居然有 \(2\) 个大王，\(2\) 个小王（一副牌原本是 \(54\) 张 _）...他随机从中抽出了 \(5\) 张牌，想测测自己的手气，看看能不能抽到顺子，如果抽到的话，他决定去买体育彩票，嘿嘿！！“红心 \(A\)，黑桃 \(3\)，小王，大王，方片\(5\)”，“Oh My God!” 不是顺子..... LL 不高兴了，他想了想，决定大\小 王可以看成任何数字，并且 \(A\) 看作 \(1\) ，\(J\) 为 \(11\)，\(Q\) 为 \(12\)，\(K\) 为 \(13\)。上面的 \(5\) 张牌就可以变成 \(“1,2,3,4,5”\)（大小王分别看作 \(2\) 和 \(4\)），”So Lucky!”。LL 决定去买体育彩票啦。 现在，要求你使用这幅牌模拟上面的过程，然后告诉我们 LL 的运气如何，如果牌能组成顺子就输出 \(true\)，否则就输出\(false\)。为了方便起见，你可以认为大小王是 \(0\)。
思路：
import java.util.*;
public class Solution {
public boolean isContinuous(int[] numbers) {
if(numbers.length < 5) {
return false;
}
//排序
Arrays.sort(numbers);
//统计大小王的数目
int zeroNum = 0;
for(int i = 0; i < 5 && numbers[i] == 0; i++) {
zeroNum++;
}
for(int i = zeroNum; i < 4; i++) {
//判断后一张牌和当前是否相等，相等返回 false
if(numbers[i + 1] == numbers[i]) {
return false;
}
//判断后一张牌是否比当前牌大 1，如果是不消耗大小王
if(numbers[i + 1] == numbers[i] + 1) {
continue;
}
//消耗大小王数目
zeroNum -= (numbers[i + 1] - numbers[i] - 1);
if(zeroNum < 0) {
//大小王耗尽，返回 false
return false;
}
}
return true;
}
}
62. 圆圈中最后剩下的数
题目描述：
每年六一儿童节，牛客都会准备一些小礼物去看望孤儿院的小朋友，今年亦是如此。HF 作为牛客的资深元老，自然也准备了一些小游戏。其中，有个游戏是这样的：首先，让小朋友们围成一个大圈。然后，他随机指定一个数 \(m\)，让编号为 \(0\) 的小朋友开始报数。每次喊到 \(m-1\) 的那个小朋友要出列唱首歌，然后可以在礼品箱中任意的挑选礼物，并且不再回到圈中，从他的下一个小朋友开始，继续 \(0...m-1\) 报数 .... 这样下去 .... 直到剩下最后一个小朋友，可以不用表演，并且拿到牛客名贵的 “名侦探柯南” 典藏版（名额有限哦!!_）。请你试着想下，哪个小朋友会得到这份礼品呢？(注：小朋友的编号是从 \(0\) 到 \(n-1\))。如果没有小朋友，请返回 \(-1\)。
思路：
该题是约瑟夫问题，该问题有一个具体的推导公式，该公式可以参考此文：约瑟夫环——公式法（递推公式）
普通解法：
使用一个布尔类型的数组 \(flags\)，\(flags[i] == true\) 代表编号为 \(i\) 的孩子退出游戏
public class Solution {
public int LastRemaining_Solution(int n, int m) {
if(n <= 0) {
return -1;
}
boolean[] flags = new boolean[n];
int num = n; //当前圈内的孩子数目
int cur = 0, j = 0; //cur 表示下个可能报数的孩子序号，j 为一轮中已经报数的孩子数目
while(true) {
//找到下一个报数孩子
while(flags[cur]) {
cur = (cur + 1) % n;
}
j++;
if(j == m) { //连续 m 个孩子报数
flags[cur] = true; //序号为 cur 的孩子退出
num--; //圈内人数减 1
j = 0; //该轮结束，j 重置为 0
}
cur = (cur + 1) % n;
if(num == 1) { //只剩下一个孩子，游戏结束
break;
}
}
while(flags[cur]) { //找到剩下的孩子的编号
cur = (cur + 1) % n;
}
return cur;
}
}
公式推导：
\(f(i, j) = (f(i-1, j) + j) \% i\)。\(f(i, j)\) 表示圈内共有 \(i\) 个人（编号分别为 \(0、1、...、i-1\)），从 \(0\) 开始报数，报到 \(j-1\) 的人退出，剩下的人继续从 \(0\) 开始报数，最终只留下的一个人，这个人的编号就是 \(f(i,j)\)。
public class Solution {
public int LastRemaining_Solution(int n, int m) {
if(n == 0) {
return -1;
}
int ret = 0; // f(1, m) 的值
for(int i = 2; i <= n; i++) {
ret = (ret + m) % i; //计算 f(i, m) 的值
}
return ret;
}
}
63. 买卖股票的最佳时机
题目描述：
给定一个数组，它的第 \(i\) 个元素是一支给定股票第 \(i\) 天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。
示例：
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
输入: [7,6,4,3,1]
输出: 0
解释: 在这种情况下, 没有交易完成, 所以最大利润为 0。
思路：
动态规划。设 \(dp[i][0]\) 为第 \(i\) 天手中没有持有股票的最大利润，\(dp[i][1]\) 为第 \(j\) 天手中持有股票的最大利润。则 $$dp[i][0] = max{dp[i-1][0], dp[i-1][1]+prices[i]}$$ $$dp[i][1]=max{dp[i-1][1]，-prices[i]} $$
其中 \(prices[i]\) 代表第 \(i\) 天的股票价格。
class Solution {
public int maxProfit(int[] prices) {
if(prices == null || prices.length == 0) {
return 0;
}
int n = prices.length;
int[][] dp = new int[n + 1][2];
dp[0][1] = Integer.MIN_VALUE;
dp[0][0] = 0;
for(int i = 1; i <= n; i++) {
dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i-1]);
dp[i][1] = Math.max(dp[i-1][1], -prices[i-1]);
}
return dp[n][0];
}
}
64. 求 1+2+3+...+n
题目描述：
求 \(1+2+3+...+n\)，要求不能使用乘除法、for、while、if、else、switch、case 等关键字及条件判断语句（A?B:C）。
思路：
利用条件 && 具有短路原则。
public class Solution {
public int Sum_Solution(int n) {
int sum = n;
boolean b = (n > 0) && ((sum += Sum_Solution(n-1)) > 0);
return sum;
}
}
65. 不用加减乘除做加法
题目描述：
写一个函数，求两个整数之和，要求在函数体内不得使用 \(+、-、*、/\) 四则运算符号。
思路：
\(a\) ^ \(b\) 表示没有考虑进位的情况下两数的和，(\(a\) & \(b\)) << \(1\) 表示两数相加时的进位。
public class Solution {
public int Add(int num1,int num2) {
if(num2 == 0) {
return num1;
}
return Add(num1 ^ num2, (num1 & num2) << 1);
}
}
66. 构建乘积数组
题目描述：
给定一个数组 \(A[0,1,...,n-1]\)，请构建一个数组 \(B[0,1,...,n-1]\)，其中 \(B\) 中的元素 \(B[i]=A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]\)，不能使用除法。
思路：
import java.util.ArrayList;
public class Solution {
public int[] multiply(int[] A) {
int n = A.length;
int[] B = new int[n];
B[0] = 1;
for(int i = 1; i < n; i++) { //从左往右乘，B[i] = A[0]*A[1]*...*A[i-1]
B[i] = B[i-1] * A[i-1];
}
int product = A[n-1];
for(int i = n - 2; i >= 0; i--) {
B[i] *= product; //B[i] = A[0]*A[1]*...*A[i-1]*A[i+1]*...*A[n-1]
product *= A[i]; //从右往左乘，product = A[n-1]*A[n-2]*...*A[i+1]
}
return B;
}
}
67. 把字符串转换成整数
题目描述：
将一个字符串转换成一个整数（实现 Integer.valueOf(string) 的功能，但是 string 不符合数字要求时返回\(0\))，要求不能使用字符串转换整数的库函数。 数值为 \(0\) 或者字符串不是一个合法的数值则返回 \(0\)。
示例：
输入：+2147483647
1a33
输出：2147483647
0
思路：
public class Solution {
public int StrToInt(String str) {
char[] letters = str.toCharArray();
int n = letters.length;
int ret = 0;
int flag = 1; //标识返回值正负号，1 代表正数，-1 代表负数
for(int i = 0; i < n; i++) {
if(i == 0) {
if(letters[0] == '+') {
flag = 1;
}else if(letters[0] == '-') {
flag = -1;
}else if('0' <= letters[0] && letters[0] <= '9') {
ret = ret * 10 + (letters[0] - '0');
}else {
return 0;
}
}else if('0' <= letters[i] && letters[i] <= '9'){
ret = ret * 10 + (letters[i] - '0');
}else {
return 0;
}
}
return flag == 1 ? ret : -ret;
}
}
68. 数中两个节点的最近公共祖先
二叉搜索树的最近公共祖先
题目描述：
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 \(T\) 的两个结点 \(p\)、\(q\)，最近公共祖先表示为一个结点 \(x\)，满足 \(x\) 是 \(p\)、\(q\) 的祖先且 \(x\) 的深度尽可能大（一个节点也可以是它自己的祖先）。”
例如，给定如下二叉搜索树: \(root = [6,2,8,0,4,7,9,null,null,3,5]\)
示例：
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- \(p\)、\(q\) 为不同节点且均存在于给定的二叉搜索树中。
思路：
结合二叉树搜索树的性质。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) {
return null;
}
if(root.val > p.val && root.val > q.val) {
return lowestCommonAncestor(root.left, p, q);
}
if(root.val < p.val && root.val < q.val) {
return lowestCommonAncestor(root.right, p, q);
}
return root;
}
}
二叉树的最近公共祖先
题目描述：
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 \(T\) 的两个结点 \(p\)、\(q\)，最近公共祖先表示为一个结点 \(x\)，满足 \(x\) 是 \(p\)、\(q\) 的祖先且 \(x\) 的深度尽可能大（一个节点也可以是它自己的祖先）。”
例如，给定如下二叉树: \(root = [3,5,1,6,2,0,8,null,null,7,4]\)
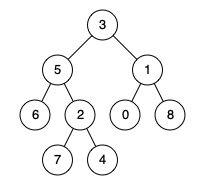
示例：
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
输出: 3
解释: 节点 5 和节点 1 的最近公共祖先是节点 3。
输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
输出: 5
解释: 节点 5 和节点 4 的最近公共祖先是节点 5。因为根据定义最近公共祖先节点可以为节点本身。
说明:
- 所有节点的值都是唯一的。
- \(p\)、\(q\) 为不同节点且均存在于给定的二叉树中。
思路：
寻找 \(p\) 和 \(q\) 节点的路径，比较两条路径找到最近的公共祖先。
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
Stack<TreeNode> pStack = new Stack<>();
Stack<TreeNode> qStack = new Stack<>();
preDfs(root, p, pStack);
preDfs(root, q, qStack);
int size = pStack.size() > qStack.size() ? qStack.size() : pStack.size();
while(--size >= 0) {
if(pStack.get(size) == qStack.get(size)) {
return pStack.get(size);
}
}
return root;
}
//前序遍历寻找将结点 node, 记录路径
public boolean preDfs(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
stack.push(root);
if(root == node) {
return true;
}
if(root.left != null) {
if(preDfs(root.left, node, stack)) {
return true;
}
}
if(root.right != null) {
if(preDfs(root.right, node, stack)) {
return true;
}
}
stack.pop();
return false;
}
}
参考
- https://cyc2018.github.io/CS-Notes/#/notes/%E5%89%91%E6%8C%87%20Offer%20%E9%A2%98%E8%A7%A3%20-%2060~68
- 《剑指OFFER 名企面试官精讲典型编程题 第2版》
剑指Offer-60~68题的更多相关文章
- 剑指offer 面试68题
面试68题: 题目:求树中两个节点的最低公共祖先 待解决...
- 《剑指offer》刷题目录
<剑指offer>刷题目录 面试题03. 数组中重复的数字 面试题04. 二维数组中的查找 面试题05. 替换空格 面试题06. 从尾到头打印链表 面试题07. 重建二叉树 面试题09. ...
- 剑指 Offer 60. n个骰子的点数
剑指 Offer 60. n个骰子的点数 把n个骰子扔在地上,所有骰子朝上一面的点数之和为s.输入n,打印出s的所有可能的值出现的概率. 你需要用一个浮点数数组返回答案,其中第 i 个元素代表这 n ...
- 浅谈《剑指offer》原题：不使用条件、循环语句求1+2+……+n
转载自:浅谈<剑指offer>原题:求1+2+--+n 如侵犯您的版权,请联系:windeal12@qq.com <剑指offer>上的一道原题,求1+2+--+n,要求不能使 ...
- 《剑指offer》算法题第十二天
今天是<剑指offer>算法题系列的最后一天了,但是这个系列并没有包括书上的所有题目,因为正如第一天所说,这些代码是在牛客网上写并且测试的,但是牛客网上并没有涵盖书上所有的题目. 今日题目 ...
- 剑指 Offer 60. n个骰子的点数 + 动态规划 + 空间优化
剑指 Offer 60. n个骰子的点数 Offer_60 题目详情 题解分析 package com.walegarrett.offer; /** * @Author WaleGarrett * @ ...
- 《剑指offer》刷题笔记
简介 此笔记为我在 leetcode 上的<剑指offer>专题刷题时的笔记整理. 在刷题时我尝试了 leetcode 上热门题解中的多种方法,这些不同方法的实现都列在了笔记中. leet ...
- 【Java】 剑指offer(60) n个骰子的点数
本文参考自<剑指offer>一书,代码采用Java语言. 更多:<剑指Offer>Java实现合集 题目 把n个骰子扔在地上,所有骰子朝上一面的点数之和为s.输入n,打 ...
- JS数据结构与算法 - 剑指offer二叉树算法题汇总
❗❗ 必看经验 在博主刷题期间,基本上是碰到一道二叉树就不会碰到一道就不会,有时候一个下午都在搞一道题,看别人解题思路就算能看懂,自己写就呵呵了.一气之下不刷了,改而先去把二叉树的基础算法给搞搞懂,然 ...
- 《剑指Offer》附加题_用两个队列实现一个栈_C++版
在<剑指Offer>中,在栈和队列习题中,作者留下来一道题目供读者自己实现,即"用两个队列实现一个栈". 在计算机数据结构中,栈的特点是后进先出,即最后被压入(push ...
随机推荐
- Keras框架下的保存模型和加载模型
在Keras框架下训练深度学习模型时,一般思路是在训练环境下训练出模型,然后拿训练好的模型(即保存模型相应信息的文件)到生产环境下去部署.在训练过程中我们可能会遇到以下情况: 需要运行很长时间的程序在 ...
- sorted排序算法
- gradle 生成 pom,引用mybatis-plus源代码到自己的工程中
一 前情概要 自己的maven工程使用mybatis-plus,然后想用热部署加载mapping文件.经过各种探索之后实现了,但是修改了xml文件后,就不断在控制台提示“mapper xxx is i ...
- 2018-8-10-C＃-判断文件编码
title author date CreateTime categories C# 判断文件编码 lindexi 2018-08-10 19:16:52 +0800 2018-2-13 17:23: ...
- 模板——伸展树 splay 实现快速分裂合并的序列
伸展操作:将treap中特定的结点旋转到根 //将序列中从左数第k个元素伸展到根,注意结点键值保存的是原序列id void splay(Node* &o, int k) { ] == NULL ...
- jekyll 添加 Valine 评论
本文告诉大家如何在自己搭建的静态博客添加 Valine 评论.在这前,我基本都是使用 多说,但是多说gg啦,所以就在找一个可以替换的评论 本来 Disqus是很好的,但是在国内很难打开,所以我就需要一 ...
- win10 uwp release 因为 Entry Point Not Found 无法启动
本文告诉大家如果在使用 release 编译时,无法启动应用,出现 Entry Point Not Found 如何让应用运行. 程序"[30760] xx.exe"已退出,返回值 ...
- Moq基础 判断方法被执行
如果想知道注入的类的某个方法被使用了几次,就可以通过 mock 提供的方法进行判断方法有没被执行或被使用多少次 本文是一个系列,具体请看 Moq基础(一) 为什么需要单元测试框架 Moq基础(二) 快 ...
- idea启用列模式的方式小结
(1)alt+鼠标左键----实现的是几个连续列要向上或者向下拉,能够同时操作多行数据. (2)Shift+alt+鼠标左键----可以实现点选跨行的列模式同时操作,而且不通行可以点选不通列,进行跨行 ...
- 基于Springboot+Junit+Mockito做单元测试
前言 前面的两篇文章讨论过< 为什么要写单元测试,何时写,写多细 >和<单元测试规范>,这篇文章介绍如何使用Springboot+Junit+Mockito做单元测试,案例选取 ...