牛客暑期第六场G /// 树形DP 最大流最小割定理

题目大意：

输入t，t个测试用例

每个测试用例输入n

接下来n行 输入u,v,w，树的无向边u点到v点权重为w

求任意两点间的最大流的总和

1.最大流最小割定理 即最大流等于最小割

2.无向树上的任意两点都可互达 也就是说 源点S可经其他任何点流到汇点T

设dist(x , y) 为在树上 x 到 y 的距离

由2能知道，S的总流量就是 n∑i=1 dis( s , i )

然后就是题解上的 S到其他各个点的距离 和 T到其他各个点的距离 中较小的即为最小割

举个栗子

4

1 2 3

1 3 4

3 4 5

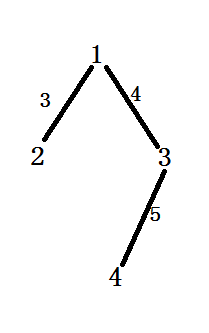
通过树形DP

ll dis[MAXN], son[MAXN], dp[MAXN];

/// dis[ i ]为从 i 点向下的分支的长度总和
/// son[ i ]为从 i 点向下的总点数(包括它本身)
/// dp[ i ]为从 i 点出发去其他所有点的长度总和

void dfs1(ll u,ll f) /// 求dis[],son[]
{
    son[u]=;
    for(int i=;i<vec[u].size();i++) {
        ll v=vec[u][i].F, w=vec[u][i].S;
        if(v==f) continue;
        dfs1(v,u);
        son[u]+=son[v];
        dis[u]+=dis[v]+son[v]*w;
    }
} 

void dfs2(int u,int f) /// 通过dis[]进行树形DP
{
    for(int i=;i<vec[u].size();i++) {
        ll v=vec[u][i].F, w=vec[u][i].S;
        if(v==f) continue;
        dp[v]=dp[u]+(n-*son[v])*w;
        dfs2(v,u);
    }
}
......

dfs1(,); dp[]=dis[]; dfs2(,);

......
/*结果为
dis[] 16 0 5 0
son[] 4  1 2 1

dp[] 16 22 16 26
*/

可以转化为一个（姑且称之为）流量图

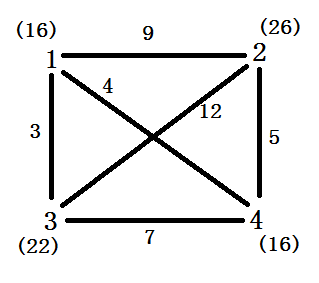
括号内的是到该点的总流量

那么 S到T的最大流 就是 两者总流量中 小的一个

sort(dp+,dp++n);
__int128 ans=;
for(int i=;i<n;i++)
     ans += dp[i]*(n-i);

当某个点x的总流量是所有点中的最小值时

那么x与其他所有点的最大流就是x的总流量

所以这里可以直接贪心 排序一下

第 i 个点与后面比它（的总流量）小的所有点（n - i 个）直接取第 i 个

也可以不用 __int128 ，开个数组模拟一下

    int ans[];
    memset(ans,,sizeof(ans));
    for(ll i=;i<n;i++) {
        ans[] += dp[i]*(n-i);
        int j=;
        while(ans[j]>=) {
            ans[j+] += ans[j]/;
            ans[j++] %= ;
        }
        len=max(len,j);
    }
    printf("Case #%d: %lld",o,ans[len]);
    for(int i=len-;i>=;i--) {
         if(ans[i]>=) printf("%lld",ans[i]);
         else if(ans[i]>=) printf("0%lld",ans[i]);
         else printf("00%lld",ans[i]);
    } printf("\n");    

完整代码

#include <bits/stdc++.h>
#define P pair<ll,ll>
#define mp(i,j) make_pair(i,j)
#define F first
#define S second
#define MAXN 100005
#define ll long long
using namespace std;

vector <P> vec[MAXN];
ll dis[MAXN], son[MAXN], dp[MAXN];
ll n, m, ans[MAXN];

void dfs1(ll u,ll f)
{
    son[u]=;
    for(int i=;i<vec[u].size();i++) {
        ll v=vec[u][i].F, w=vec[u][i].S;
        if(v==f) continue;

        dfs1(v,u);

        son[u]+=son[v];
        dis[u]+=dis[v]+son[v]*w;
    }
}

void dfs2(int u,int f)
{
    for(int i=;i<vec[u].size();i++) {
        ll v=vec[u][i].F, w=vec[u][i].S;
        if(v==f) continue;

        dp[v]=dp[u]+(n-*son[v])*w;

        dfs2(v,u);
    }
}

int main()
{
    int t; scanf("%d",&t);
    for(int o=;o<=t;o++) {
        for(int i=;i<=n;i++) vec[i].clear();
        memset(dis,,sizeof(dis));
        memset(son,,sizeof(son));
        memset(dp,,sizeof(dp));

        scanf("%lld",&n);
        for(int i=;i<n;i++) {
            ll u,v,w; scanf("%lld%lld%lld",&u,&v,&w);
            vec[u].push_back(mp(v,w));
            vec[v].push_back(mp(u,w));
        }

        dfs1(,); dp[]=dis[]; dfs2(,);
        sort(dp+,dp++n);

        int len=;
        memset(ans,,sizeof(ans));
        for(ll i=;i<n;i++) {
            ans[] += dp[i]*(n-i);
            int j=;
            while(ans[j]>=) {
                ans[j+] += ans[j]/;
                ans[j++] %= ;
            }
            len=max(len,j);
        }

        printf("Case #%d: %lld",o,ans[len]);
        for(int i=len-;i>=;i--) {
            if(ans[i]>=) printf("%lld",ans[i]);
            else if(ans[i]>=) printf("0%lld",ans[i]);
            else printf("00%lld",ans[i]);
        } printf("\n");
    }

    return ;
}

数组模拟

#include <bits/stdc++.h>
#define P pair<int,int>
#define mp(i,j) make_pair(i,j)
#define F first
#define S second
#define MAXN 100005
using namespace std;
vector <P> vec[MAXN];
int son[MAXN];
int n, m;
__int128 dis[MAXN], dp[MAXN];

void dfs1(int u,int f)
{
    son[u]=;
    for(int i=;i<vec[u].size();i++) {
        int v=vec[u][i].F, w=vec[u][i].S;
        if(v==f) continue;

        dfs1(v,u);

        son[u]+=son[v];
        dis[u]+=dis[v]+son[v]*w;
    }
}

void dfs2(int u,int f)
{
    for(int i=;i<vec[u].size();i++) {
        int v=vec[u][i].F, w=vec[u][i].S;

        if(v==f) continue;

        dp[v]=dp[u]+(n-*son[v])*w;

        dfs2(v,u);
    }
}

void print(__int128 ans)
{
    if(ans>) print(ans/);
    printf("%c",''+ans%);
}

int main()
{
    int t; scanf("%d",&t);
    for(int o=;o<=t;o++) {

        for(int i=;i<=n;i++) vec[i].clear();
        memset(dis,,sizeof(dis));
        memset(son,,sizeof(son));
        memset(dp,,sizeof(dp));

        scanf("%d",&n);
        for(int i=;i<n;i++) {
            int u,v,w; scanf("%d%d%d",&u,&v,&w);
            vec[u].push_back(mp(v,w));
            vec[v].push_back(mp(u,w));
        }

        dfs1(,); dp[]=dis[]; dfs2(,);

        sort(dp+,dp++n);
        __int128 ans=;
        for(int i=;i<n;i++)
            ans += dp[i]*(n-i);

        printf("Case #%d: ",o);
        print(ans);printf("\n");
    }

    return ;
}

__int128