枚举 + exgcd

题意：已知xi=(a*xi-1+b) mod 10001，且告诉你x1,x3.........x2*t-1,让你求出其偶数列

思路分析 ： 题目所要求的的是对 10001 取余，由模运算的性质可知，a 在经过取模后一定是 0 - 10000 范围内的一个数，那么我们就可以枚举 a

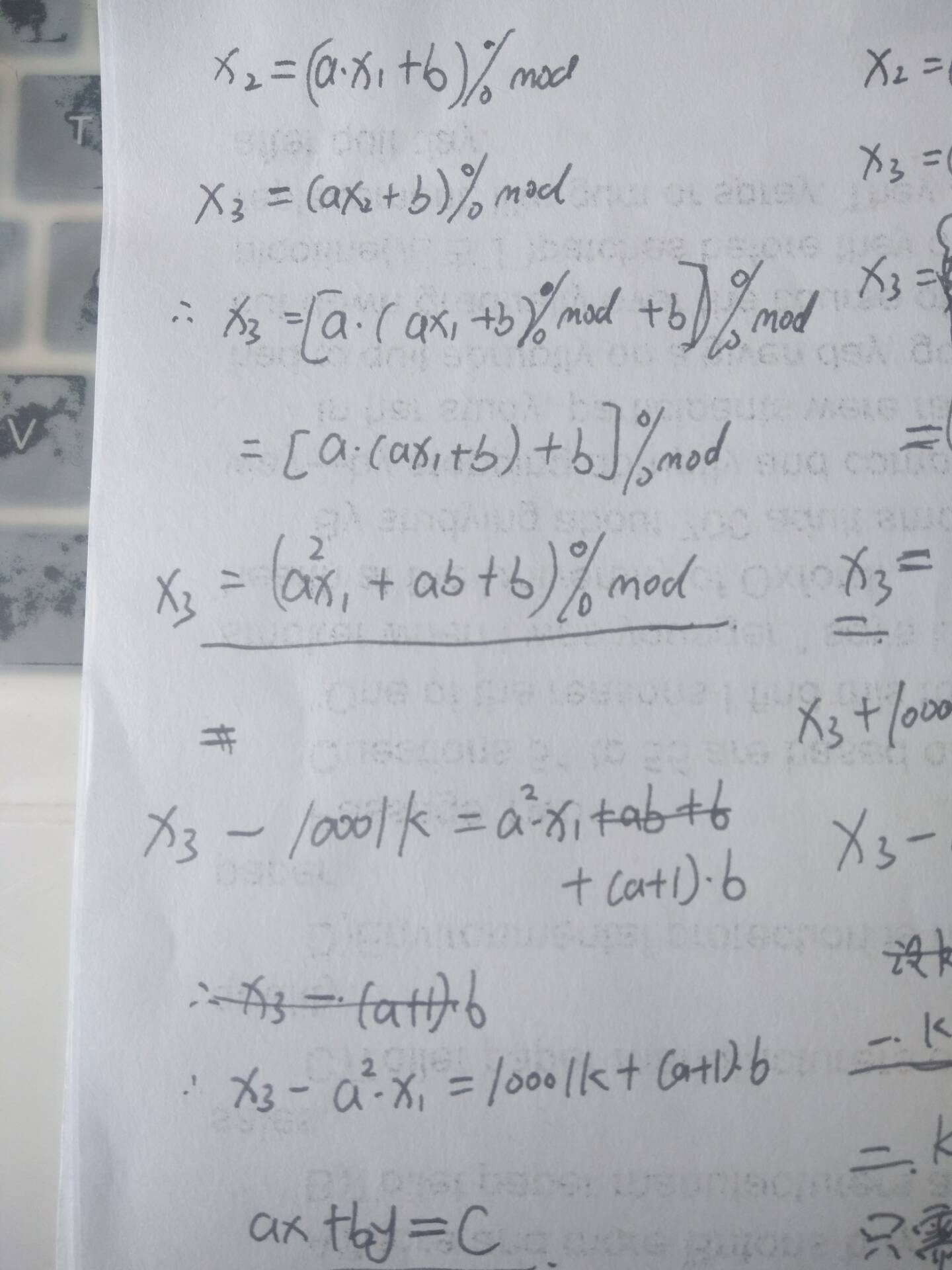
在利用 x2, x3 的式子代入化简，最终得到的式子是类似 exgcd 的，直接求就可以。

代码示例 ：

#define ll long long
const ll maxn = 1e6+5;
const ll mod = 10001;
const double eps = 1e-9;
const double pi = acos(-1.0);
const ll inf = 0x3f3f3f3f;

ll n;
ll pre[105];
ll mid[205];

void exgcd(ll a, ll b, ll &g, ll &x, ll &y){
    if (b == 0){ g = a; x = 1; y = 0;}
    else {exgcd(b, a%b, g, y, x); y -= x*(a/b);}
}

int main() {
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    cin >> n;
    for(ll i = 1; i <= n; i++){
        scanf("%lld", &pre[i]);
    }
    ll g, b, k;
    for(ll i = 0; i <= 10000; i++){
        ll f = (pre[2]-i*i*pre[1]);

        exgcd(mod, i+1, g, k, b);
        if (f % g) continue;
        b = b*(f/g)%mod;

        mid[1] = pre[1];
        for(ll j = 2; j <= 2*n; j++){
            mid[j] = (i*mid[j-1]+b+mod)%mod;
        }
        ll sign = 0;
        for(ll j = 1; j <= 2*n; j += 2){
            if (mid[j] != pre[(j+1)/2]){
                sign = 1; break;
            }
        }
        if (!sign){
            break;
        }
    }
    for(ll j = 2; j <= 2*n; j += 2){
        printf("%lld\n", mid[j]);
    }
    return 0;
}