【Math】高数-一个有趣的旋转体体积与面积

Go confidently in the direction of your dreams. Live the life you've imagined.

题目
设曲线 \(y = \tfrac{1}{x}\) (1\(\leq\)x\(\leq\)+\(\infty\)) 与X 轴之间的区域为D.
求D绕X轴旋转一周的旋转体的体积V和面积A。
图形如下

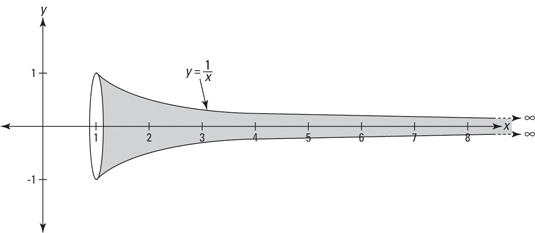
画出图形容易计算体积
\[ V =
\begin{aligned}
\int_1 ^{+\infty} \pi ( \tfrac{1}{x} )^2 \mathrm{d} x
\end{aligned}
= \pi
\]

体积公式
\[ A = \int_1^{+\infty} 2 \pi y \sqrt{1+(y^{'})^2} \mathrm{d} x = 2 \pi \int_1^{+\infty} \tfrac{1}{x} \sqrt{1+\tfrac{1}{x^4}}\mathrm{d} x \geq 2 \pi \int_1^{+\infty} \tfrac{1}{x} \mathrm{d} x = {+\infty}
\]
即体积V = \(\pi\) ,表面积A = \(+\infty\)
容积有限，表面积却无限，
Gabriel's horn (also called Torricelli's trumpet) is a geometric figure which has infinite surface area but finite volume.
也就是说往这个喇叭中装满油漆，但是里面的油漆却无法将喇叭的内侧涂一遍。
Since the horn has finite volume but infinite surface area, there is an apparent paradox that the horn could be filled with a finite quantity of paint and yet that paint would not be sufficient to coat its inner surface.
这悖论挺有意思的，
The paradox is resolved by realizing that a finite amount of paint can in fact coat an infinite surface area — it simply needs to get thinner at a fast enough rate.
这是Gabriel's Horn，圣经中天使之一，上帝传送好消息给人类的使者。