hdu 2844 混合背包【背包dp】

http://acm.hdu.edu.cn/showproblem.php?pid=2844

题意：有n种纸币面额(a1,a2,...an),每种面额对应有(c1,c2,...cn)张。问这些钱能拼成1-m中多少种值。

题解：背包dp问题。若ci=1,是01背包，若ci*ai>=m则是完全背包，否则是多重背包。（详见《背包九讲》）

先复习一下三种简单背包形式：

　01背包（F[v] ← max{F[v], F[v −Ci] +Wi} ）：

　

　　

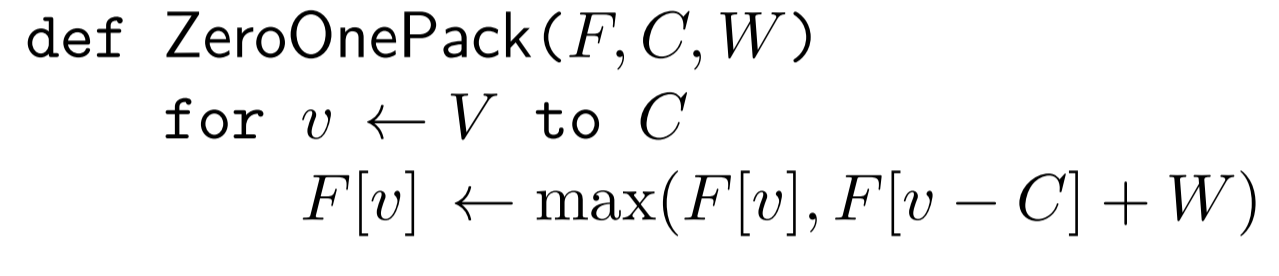
　完全背包（F[i, v] = max(F[i − 1, v], F[i, v −Ci] +Wi)）:

　 

　多重背包（利用二进制思想转化为01背包）：

　　

利用三种背包形式就可以轻松解决此题：

　　

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<queue>
 #include<vector>
 using namespace std;

 int f[];
 int c[],a[];
 int n,m;

 void ZeroOnePack(int w,int v)
 {
     for(int j=m;j>=v;j--)
         f[j]=max(f[j],f[j-w]+v);
 }

 void CompletePack(int w,int v)
 {
     for(int j=v;j<=m;j++)
         f[j]=max(f[j],f[j-w]+v);
 }

 void MultiplePack(int w,int v,int c)
 {
     int k=;
     while(k<c)
     {
         ZeroOnePack(k*w,k*v);
         c=c-k;k*=;
     }
     ZeroOnePack(c*w,c*v);
 }

 int main()
 {
     while(scanf("%d%d",&n,&m)==)
     {
         memset(f,,sizeof(f));
         if(n==) break;
         for(int i=;i<=n;i++) scanf("%d",&a[i]);
         for(int i=;i<=n;i++) scanf("%d",&c[i]);
         for(int i=;i<=n;i++){
             if(c[i]==)
                 ZeroOnePack(a[i],a[i]);
             else if(c[i]*a[i]>=m)
                 CompletePack(a[i],a[i]);
             else
                 MultiplePack(a[i],a[i],c[i]);
         }
         int ans=;
         for(int i=;i<=m;i++)
             if(f[i]==i) ans++;
         printf("%d\n",ans);
     }
     return ;
 }