AcWing 849. Dijkstra求最短路 I 朴素 邻接矩阵 稠密图

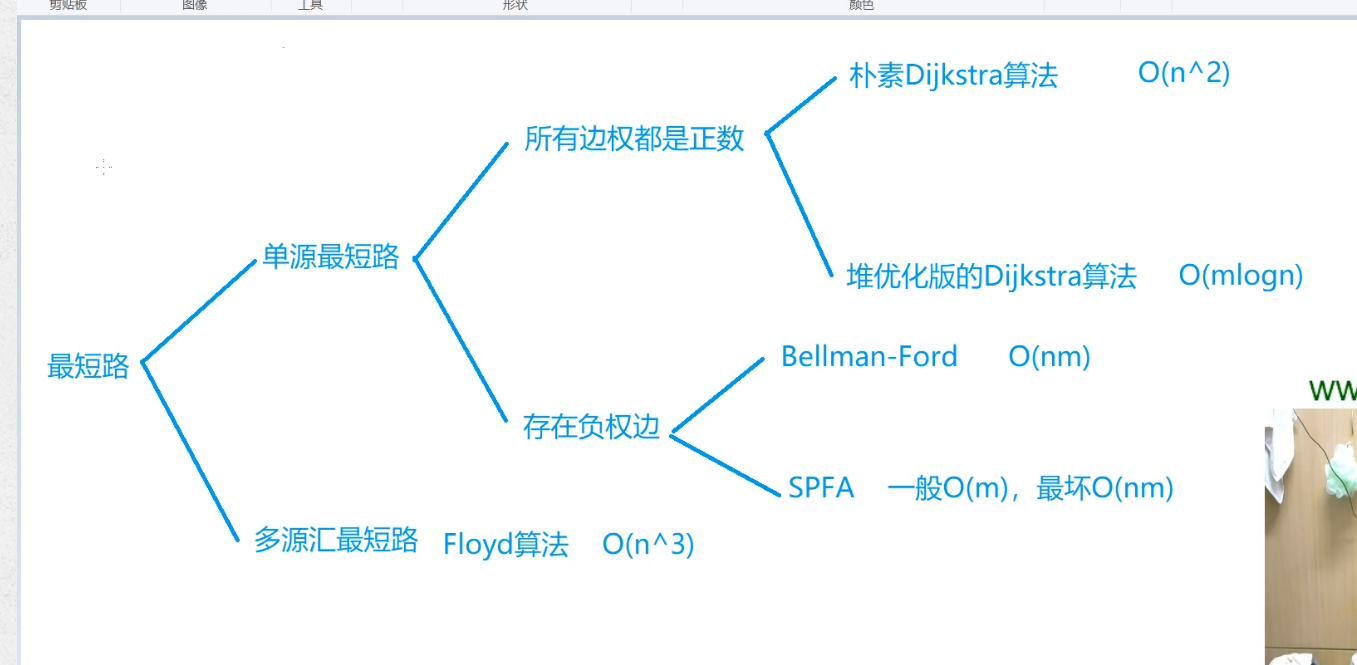
//朴素Dijkstra 边权都是正数  稠密图：点和边差的比较多
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N = ;
int n, m;
int g[N][N];//邻接矩阵       稠密图
int dist[N];//距离      从1到每个点的距离  当前的最短距离
bool st[N];
//每一次 找到当前没有确定最短路长度的点当中距离最小的那一个，
//然后用1到j的距离去和1到t的距离+t到h的距离比较，如果存在边，就会正常比较，如果不存在边，后者会变为正无穷
//相当于没比较
int dijkstra() {
    memset(dist, 0x3f, sizeof dist);//先把所有的距离初始化为正无穷
    dist[] = ;//把一号点初始化为0
    for (int i = ; i < n - ; i ++ ) {//迭代n次
        //每一次先找最小值 找到当前没有确定最短路长度的点当中距离最小的那一个
        int t = -; //表示还没有确认1d
        for (int j = ; j <= n; j ++ )//遍历所有点
            //如果当前点还没有确定最短路，或者t还没有赋值，或者当前不是最短的
            if (!st[j] && (t == - || dist[t] > dist[j]))//找还没有确定最短长度的点当中距离1最小的那一个
                t = j;//遍历循环所有点，找到最小的
        if(t==n) break;//说明1和n之间的边的权重最下
        for (int j = ; j <= n; j ++ )
            //用从1到t的距离加上t到j这条边来更新1到j这条边  每次都更新
            dist[j] = min(dist[j], dist[t] + g[t][j]);
        st[t] = true;
    }
    if (dist[n] == 0x3f3f3f3f) return -;//说明1和n不连通
    return dist[n];//返回n的最短距离
}
int main() {
    scanf("%d%d", &n, &m);
    memset(g, 0x3f, sizeof g);//初始化
    while (m -- ) {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        g[a][b] = min(g[a][b], c);//处理重边，保留长度最短的边    权重
    }
    printf("%d\n", dijkstra());
    return ;
}