Ex 3_25 图中每个顶点有一个相关价格..._十一次作业

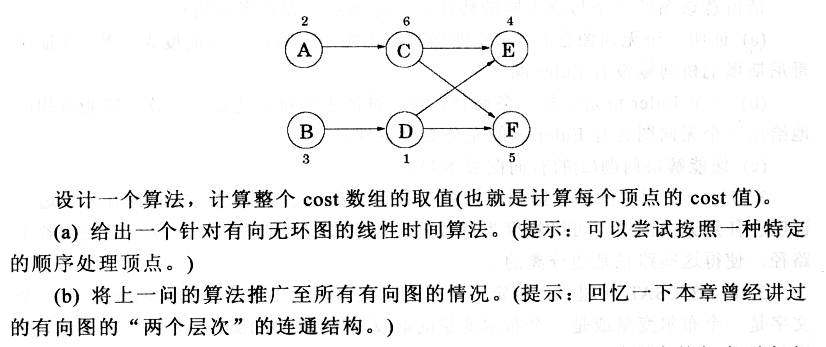
(a)首先对有向无环图进行拓扑排序,再按拓扑排序的逆序依次计算每个顶点的cost值，每个顶点的cost值为自身的price值与相邻顶点间的cost值得最小值

(b)求出图中的每一个强连通分量，并把所有得强连通分量看成是一个有向无环图,设每一个强连通分量的price值为该强连通分量中顶点的最小的price值。然后再按(a)中的步骤处理DAG

 package org.xiu68.ch03.ex11;

 import java.util.ArrayDeque;
 import java.util.ArrayList;
 import java.util.List;
 import java.util.Stack;

 public class Ex3_25 {
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         int[][] edges=new int[][]{
             {0,0,1,0,0,0},
             {0,0,0,1,0,0},
             {0,0,0,0,1,1},
             {0,0,0,0,1,1},
             {0,0,0,0,0,0},
             {0,0,0,0,0,0}
         };
         int[] price=new int[]{2,3,6,1,4,5};
         MGraph2 m1=new MGraph2(edges, price);
         m1.getCost();
         System.out.println("*****************");
         m1.getSccCost();
         //输出
         /*
         cost[0]:2
         cost[1]:1
         cost[2]:4
         cost[3]:1
         cost[4]:4
         cost[5]:5
         *****************
         cost[0]=2
         cost[1]=1
         cost[2]=4
         cost[3]=1
         cost[4]=4
         cost[5]=5
         */
         System.out.println("*******************");
         int[][] edges1=new int[][]{
             {0,0,0,0,0,0,0},
             {1,0,0,1,0,0,0},
             {1,0,0,1,0,0,0},
             {0,0,0,0,1,1,0},
             {0,0,0,1,0,0,1},
             {0,0,0,1,0,0,1},
             {0,0,0,0,1,1,0}
         };
         int[] price1=new int[]{6,7,9,5,3,4,2};
         MGraph2 m2=new MGraph2(edges1, price1);
         m2.getSccCost();
         //输出
         /*
         cost[0]=6
         cost[1]=2
         cost[2]=2
         cost[3]=2
         cost[4]=2
         cost[5]=2
         cost[6]=2
         */
     }

 }

 class MGraph2{
     private int[][] edges;                //有向图
     private int[][] rEdges;                //有向图的反向图
     private int vexNum;                    //顶点数量
     private int[] price;                //每个顶点的相对价格
     private int[][] sccEdges;            //强连通分量(DAG)之间的关系
     private Stack<Integer> stack;        //存储反向图深度优先遍历的post值

     public MGraph2(int[][] edges,int[] price){
         this.edges=edges;
         this.vexNum=edges.length;
         this.price=price;
         this.stack=new Stack<>();
         this.rEdges=new int[vexNum][vexNum];
         this.sccEdges=new int[vexNum][vexNum];

         //求原图的反向图
         for(int i=0;i<vexNum;i++){
             for(int j=i+1;j<vexNum;j++){
                 rEdges[i][j]=edges[j][i];
                 rEdges[j][i]=edges[i][j];
             }
         }
     }

     //**********************************************************
     //针对有向无环图，获取每个顶点的cost值
     public void getCost(){
         ArrayDeque<Integer> queue=new ArrayDeque<Integer>();    //存取拓扑排序的逆序
         int[] cost=new int[vexNum];
         for(int i=0;i<vexNum;i++)
             cost[i]=price[i];
         topoSort(queue,edges,vexNum);

         //依次处理每个顶点,每个顶点取自身的price值和邻接点的cost值得最小值
         while(!queue.isEmpty()){
             int v=queue.poll();
             for(int i=0;i<vexNum;i++){
                 if(edges[v][i]==1 && cost[i]<cost[v])
                     cost[v]=cost[i];
             }
         }
         for(int i=0;i<vexNum;i++)
             System.out.println("cost["+i+"]:"+cost[i]);
     }
     //求拓扑排序的逆序
     public void topoSort(ArrayDeque<Integer> queue,int[][] edgeArray,int vertexNum){
         boolean[] visited=new boolean[vertexNum];
         for(int i=0;i<vertexNum;i++){
             if(!visited[i])
                 topoDFS(queue,visited,edgeArray,vertexNum,i);
         }
     }
     //深度优先遍历求拓扑排序
     public void topoDFS(ArrayDeque<Integer> queue,boolean[] visited,int[][] edgeArray,int vertexNum,int v){
         visited[v]=true;
         for(int i=0;i<vertexNum;i++){
             if(edgeArray[v][i]==1 && !visited[i]){
                 topoDFS(queue,visited,edgeArray,vertexNum,i);
             }
         }
         queue.add(v);
     }

     //****************************************************************
     //针对所有有向图的情况,获取每个顶点的cost值
     public void getSccCost(){
         rDFSTraverse();                                    //先对反向图进行深度优先遍历

         List<List<Integer>> sccs=new ArrayList<>();        //存放每一个强连通部件对应的顶点

         boolean[] visited=new boolean[vexNum];            //记录深度优先遍历原图过程中非当前强连通分量已经访问的顶点
         int[] visitedN=new int[vexNum];                    //记录顶点属于第几个强连通分量
         int n=0;                                        //第几个强连通部件    

         for(int i=0;i<vexNum;i++){
             visitedN[i]=-1;
         }

         //依次出栈,并从该顶点开始对原图进行深度优先遍历,获取每个强连通分量对应的顶点
         //并获取DAG之间的关系
         while(!stack.isEmpty()){
             int v=stack.pop();
             if(!visited[v]){
                 sccs.add(new ArrayList<Integer>());
                 List<Integer> vexs=new ArrayList<>();    //获取第n个强连通分量的顶点

                 sccDFS(visited,visitedN,v,sccs,vexs,/*isSinkSCC,*/n);
                 //为了知道遍历第n个强连通分量之前已经访问过哪些顶点
                 //遍历完一个强连通分量再设visited值
                 for(int i=0;i<vexs.size();i++){
                     visited[vexs.get(i)]=true;
                 }
                 n++;
             }
         }

         int[] sccPrice=new int[sccs.size()];
         int[] sccCost=new int[sccs.size()];
         //将每个强连通分量的price值设为强连通分量中price值最小的顶点的price值
         for(int i=0;i<sccs.size();i++){
             sccPrice[i]=Integer.MAX_VALUE;
             for(int j=0;j<sccs.get(i).size();j++){
                 //sccs.get(i).get(j) 第i个强连通分量的第j个顶点
                 if(price[sccs.get(i).get(j)]<sccPrice[i]){
                     sccPrice[i]=price[sccs.get(i).get(j)];
                 }
             }
         }

         //对DAG进行拓扑排序
         ArrayDeque<Integer> topoQueue=new ArrayDeque<>();
         topoSort(topoQueue, sccEdges, sccs.size());

         for(int i=0;i<sccs.size();i++)
             sccCost[i]=sccPrice[i];

         //topoSort(topoQueue,edges,vexNum);
         ////依次处理DAG中每个顶点,每个顶点取自身的price值和邻接点的cost值得最小值
         while(!topoQueue.isEmpty()){
             int v=topoQueue.poll();
             for(int i=0;i<sccs.size();i++){
                 if(sccEdges[v][i]==1 && sccCost[i]<sccCost[v])
                     sccCost[v]=sccCost[i];
             }
         }

         //visitedN[i] 第i个顶点在第几个强连通分量中
         for(int i=0;i<vexNum;i++)
             System.out.println("cost["+i+"]="+sccCost[visitedN[i]]);
     }

     //对原图进行深度优先遍历
     //在汇点强连通部件中对某个顶点进行深度优先遍历则刚好访问该强连通部件的所有顶点
     private void sccDFS(boolean[] visited,int[] visitedN,int v,List<List<Integer>> sccs,
             List<Integer> vexs,/*boolean[] isSinkSCC,*/int n){
         sccs.get(n).add(v);
         vexs.add(v);
         visitedN[v]=n;
         for(int i=0;i<vexNum;i++){
             if(edges[v][i]==1){
                 //若遍历到其他强连通分量的顶点说明该强连通分量不是汇点强连通分量
                 if(visited[i]){
                     //i为其他强连通分量的顶点,所以当前强连通分量有一条边指向i所在的强连通分量
                     sccEdges[n][visitedN[i]]=1;
                 }else if(visitedN[i]!=n){
                     sccDFS(visited,visitedN,i,sccs,vexs,/*isSinkSCC,*/n);
                 }
             }
         }//for
     }
     //***********************************************************
     /*
      * 对反向图进行深度优先遍历,post值最大的顶点将位于反向图中的一个源点强连通部件，
      * 也就是原图中的某个汇点连通部件的某个顶点
      * 按post值从小到大,压入栈中
      */
     public void rDFSTraverse(){
         boolean[] visited=new boolean[vexNum];
         for(int i=0;i<vexNum;i++){
             if(!visited[i]){
                 rDFS(visited,stack,i);
             }
         }
     }
     //对反向图做深度优先遍历
     private void rDFS(boolean[] visited,Stack<Integer> stack,int v){
         visited[v]=true;
         for(int i=0;i<vexNum;i++){
             if(rEdges[v][i]==1 && !visited[i]){
                 rDFS(visited,stack,i);
             }
         }
         stack.push(v);
     }
 }